Local Search Algorithm
많은 최적화 문제에서, 경로(Path)는 중요하지 않으며, Goal state가 Solution이 된다.
Goal state인 상태에서 그 State Space는 "완전한(Complete)" 구성 집합으로 이루어져있다.
이를 알았으니, 최적화 문제에서 Goal state를 솔루션으로 찾기 위해
=>
제약 조건을 만족하는 구성( configuration satisfying constraints )을 찾거나 (ex : n-queens 문제)
최적 구성(optimal configuration)을 찾아야한다. ( ex: traveling salesperson 문제)


이러한 경우 반복적인 개선 알고리즘(iterative improvement Algorithm)을 사용할 수 있다 : 단일 현재 상태(single current state)를 유지하고 그것을 개선하려고 시도하는 것이다.
- 반복적인 개선 알고리즘은 initail solution (또는 current state)에서 시작하여 반복적으로 작은 변경을 통해 그것을 개선하려고 하는 최적화 기법이다.
반복 개선 알고리즘은 상수 공간(Constant Space), 온라인 및 오프라인 검색에 적합하다.
- 이러한 알고리즘은 일반적으로 일정한 양의 메모리 (또는 공간)를 사용하기 때문에 저장 요구 사항 측면에서 효율적이다.
- 온라인 (실시간) 및 오프라인 (미리 계산된) 검색 시나리오 모두에서 사용할 수 있다.
"State"가 스스로(yourself)인 경우, 더욱 피할 수 없다(unavoidable). (i.e. learning) :
- 이 말이 무슨 말인가하면, 최적화의 "상태" 또는 대상이 자신(yourself)일 때, 반복적인 개선은 자연스럽고 거의 피할 수 없는 접근 방식이라는 것을 나타낸다.
Hill Climbing
"Hill Climbing"은 로컬 검색 알고리즘 중 하나로, 주어진 문제의 해결책을 찾기 위해 현재 상태의 이웃 상태를 반복적으로 탐색하면서 최적의 상태로 이동하는 방법이다.
Hill Climbing은 간단하면서도 일반적인 아이디어를 기반으로 한다. :
- Start wherever : 어디서든 시작할 수 있다. 즉, 초기 상태는 무작위로 선택되거나 특정 기준에 따라 선택될 수 있다.
- Repeat: move to the best neighboring state
- 현재 상태의 이웃 상태 중에서 가장 좋은 상태로 이동한다. 가장 좋은(best)이라는 것은 문제의 목표에 따라 다를 수 있다. 예를 들어, 최대화 문제의 경우 가장 높은 값을 가진 이웃 상태로, 최소화 문제의 경우 가장 낮은 값을 가진 이웃 상태로 이동한다.
- If no neighbors better than current, quit : 현재 상태보다 더 나은 이웃 상태가 없다면 알고리즘을 종료한다. 이는 현재 상태가 지역 최적해(local solution)라는 것을 의미한다.
Hill Climbing은 그 이름에서 알 수 있듯이 언덕을 오르는 것과 유사한 방식으로 작동한다. 현재 위치에서 주변을 탐색하여 가장 높은 지점으로 이동하고, 더 이상 높은 지점이 없을 때까지 이 과정을 반복한다. 그러나 이 알고리즘의 한계는 지역 최적해에 갇힐 수 있다는 것이다. 즉, 전역 최적해를 찾지 못하고 언덕의 일부 지점에서 멈출 수 있다.
Heuristic for n-Queens Problem

n-Queens 문제는 체스판에서 n개의 퀸을 배치하는 문제로, 어떤 두 퀸도 서로를 공격할 수 없는 위치에 배치하는 것이 목표이다.
- 목표(Goal): n 개의 퀸을 체스판에 배치하는데, 충돌(conflict)가 없어야한다. 즉, 어떤 두 퀸도 서로를 공격할 수 없어야한다.
- 퀸은 체스에서 가로, 세로, 대각선 방향으로 움직일 수 있기 때문에 이러한 방향으로 다른 퀸과 겹치지 않도록 배치해야한다.
- 상태(States): 체스판에 배치된 n개의 퀸을 나타낸다. 각 열(column)에는 하나의 퀸만 있어야한다.
- 행동(Actions): 퀸을 열 내에서(in its columns) 움직인다.
- 가능한 행동은 각 퀸을 그것의 열 내에서 움직이는 것이다. 왜냐하면 하나의 column에는 하나의 퀸만 존재해야 하기 때문이다. 즉, 퀸은 세로 방향의 한 방향으로만 움직일 수 있다.
- 휴리스틱 값 함수(Heuristic value function): 충돌 횟수(number of conflicts)
- 충돌은 두 퀸이 서로를 공격할 수 있는 위치에 있을 때 발생한다. 충돌의 수가 적을수록 그 상태는 목표 상태에 더 가깝다고 볼 수 있다.
Hill-climbing Algorithm
function HILL-CLIMBING(problem) returns a state
current ← make-node(problem.initial-state)
loop do
neighbor ← a highest-valued successor of current
if neighbor.value ≤ current.value then
return current.state
current ← neighbor
Hill-climbing 알고리즘의 의사코드는 위와 같다. 현재 상태에서 가장 좋은 이웃 상태로 반복적으로 이동하여 최적의 상태를 찾는 방식으로 작동한다.
function HILL-CLIMBING(problem) returns a state
- `HILL-CLIMBING`이라는 함수가 정의되어 있으며, 입력으로 `problem`을 받아 결과로 상태(state)를 반환한다.
current ← make-node(problem.initial-state)
- 초기 상태(initial state)를 `current`로 설정한다.
loop do
- 루프(반복문)를 시작한다.
neighbor ← a highest-valued successor of current
- 현재 상태 `current`의 이웃 상태 중에서 가장 높은 값을 가진 상태를 `neighbor`로 선택합니다.
if neighbor.value ≤ current.value then
- 만약 `neighbor`의 값이 `current`의 값보다 작거나 같다면 (즉, 더 나은 상태가 아니라면)
return current.state
- 현재 상태 `current`를 반환하고 알고리즘을 종료한다.
current ← neighbor
- 그렇지 않다면(즉, 더 나은 상태라면 ; current 값보다 neighbor 값이 크다면), `current`를 `neighbor`로 업데이트한다.
“Like climbing Everest in thick fog with amnesia”
Hill-climbing 알고리즘은 현재 위치에서 가장 높은 지점으로만 이동하기 때문에, 전체 지형을 볼 수 없는 상태에서 마치 짙은 안개가 낀 에베레스트 산을 오르는 것과 유사하다.( Like climbing Everest in thick fog )
또한 "amnesia"는 알고리즘이 이전에 방문한 상태나 경로를 기억하지 않는다는 것을 나타낸다. 따라서 이 알고리즘은 지역 최적해에 갇힐 수 있으며, 전역 최적해를 찾지 못할 수도 있다.
Global and Local Maxima
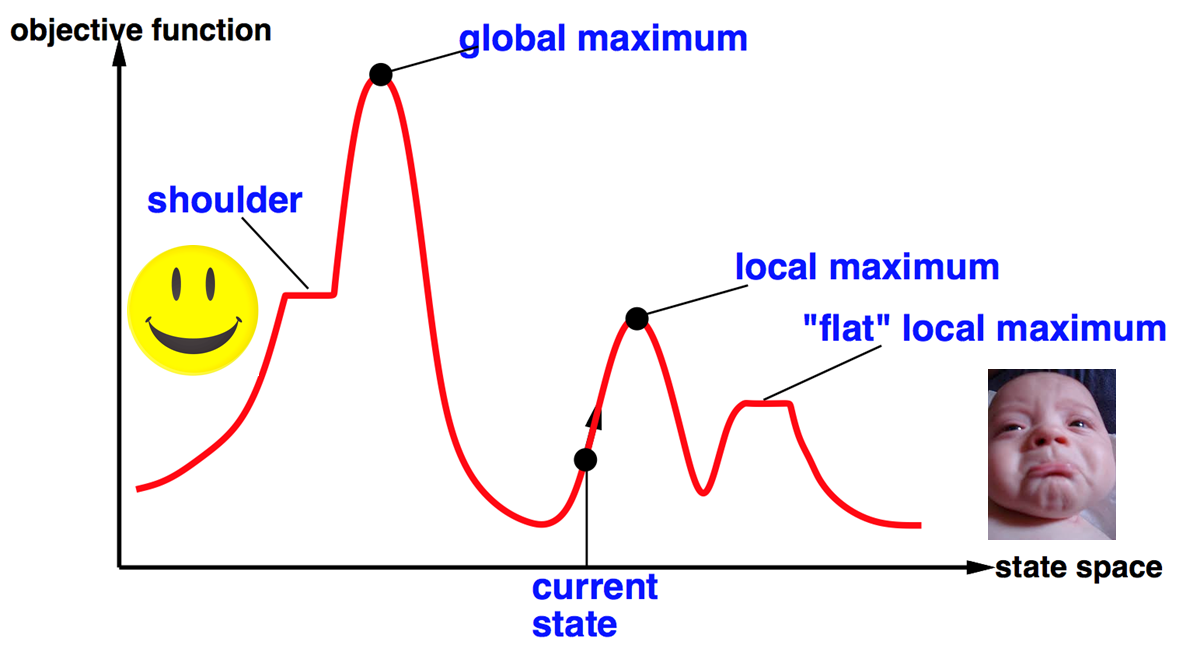
"Global and Local Maxima"는 최적화 문제에서 중요한 개념이다. 최적화 문제에서 목표는 주어진 함수의 최대값 (또는 최소값)을 찾는 것이다. 이때, 함수의 전체 정의역에서의 최대값을 "전역 최대값 (Global Maxima)"이라고 하며, 함수의 일부 구간에서의 최대값을 "지역 최대값 (Local Maxima)"이라고 한다.
로컬 검색 알고리즘은 종종 지역 최대값에 갇히게 되는데, 지역 최대값에 빠지지 않기 위해서는 다음과 같은 방법을 시도해 볼 수 있다.
- Random restarts :
- find global optimum : 무작위 재시작을 사용해 여러 다른 초기 상태에서 알고리즘을 여러 번 실행하면 당연하게도(duh) 전역 최대값을 찾을 확률을 높일 수 있다.
- Random sideways moves :
- Escape from shoulders: "Shoulder"는 함수의 그래프에서 평평한 부분을 나타낸다. shoulder 부분에서는 지역 최대값에 갇히기 쉽다. sideways move는 주변(좌우)로의 움직임을 허용한다는 것인데 shoulder의 좌우 side로 무작위하게 움직여서 shoulder에서 벗어나 지역 최대값에서 벗어날 수 있다.
- Loop forever on flat local maxima: 그러나 이 기법의 단점은 평평한 지역 최대값,shoulder에서 영원히 루프를 돌 수 있다는 것이다. shoulder 에서만 무한으로 왔다갔다 할 수 있으므로 알고리즘이 평평한 shoulder 지역에서 지역 최대값에 갇히지 않고 빠져나갈 수 있는 적절한 방법을 사용할 수 있는 것이 중요하다.
'전공 공부 > 인공지능(Artificial Intelligence)' 카테고리의 다른 글
| [인공지능] Propositional Logic - 3 (0) | 2023.10.08 |
|---|---|
| [인공지능] Propositional Logic - 2 (0) | 2023.10.08 |
| [인공지능] Propositional Logic - 1 (1) | 2023.09.27 |
| [인공지능] Local Search - 3 (0) | 2023.09.25 |
| [인공지능] Local Search - 2 (0) | 2023.09.25 |



