Backtracking Search
Backtracking Search
- 기본 개념
- Backtracking search는 CSPs (Constraint Satisfaction Problems)를 해결하기 위한 기본적인 비정보화된 알고리즘(basic uninformed algorithm)이다.
- Idea 1: 한 번에 하나의 변수(One variable at a time)
- 변수 할당은 교환 가능(commutative)하므로 순서를 고정(fix ordering)한다.
- 즉, [WA = red then NT = green]은 [NT = green then WA = red]와 동일하다.
- 각 단계에서 단일 변수에 대한 할당만 고려할 필요가 있다.
- Idea 2: 진행 중에 제약 조건 확인(Check constraints as you go)
- 즉, 이전 할당과 충돌하지 않는 값만 고려한다.
- 제약 조건을 확인하기 위해 일부 계산을 수행해야 할 수도 있다.
- "Incremental goal test"(증분적 목표 테스트)라고 한다.
- 깊이 우선 탐색(DFS)과 이 두 가지 개선 사항(Idea 1,2)을 결합한 것이 backtracking search이다.
- n-queens 문제의 경우, n이 대략 25일 때 해결할 수 있다.
Backtracking Example
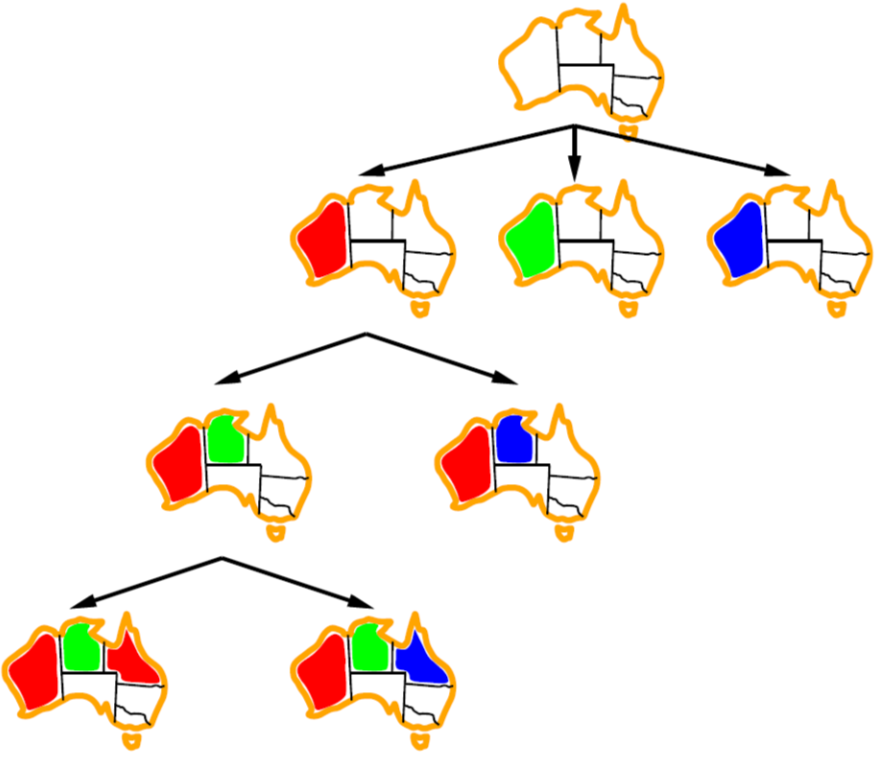
Improving Backtracking
- 일반 목적의 아이디어(general-purpose idea)는 속도의 큰 향상을 가져온다.
- Filtering (필터링) :
- 불가피한 실패(inevitable failure)를 조기에 감지(detect)할 수 있을까? 필터링은 할당되지 않은 변수의 도메인을 추적하고 나쁜 옵션을 제외한다.
- Ordering (정렬) :
- 값을 시도(should try)해야 하는 순서(order)는 어떻게 될까? 특정 순서에 따라 변수의 값을 시도하면 탐색 시간을 줄일 수 있다.
- Structure (구조) :
- 문제의 구조를 활용(exploit)할 수 있을까? 문제의 특정 구조를 이해하고 활용하면 더 효율적인 탐색이 가능하다.
Filtering: Forward Checking
Forward Checking은 Backtracking 탐색을 개선하기 위한 방법 중 하나로, 미리 제약 조건을 확인하여 불필요한 탐색을 줄이는 데 도움을 준다.

- Filtering:
- 할당되지 않은 변수의 도메인을 추적하고 나쁜(bad)옵션을 제외(cross off)한다. 이는 변수에 할당할 수 있는 가능한 값의 집합을 유지하면서, 이미 할당된 변수의 값과 충돌하는 값을 제외하는 것을 의미한다.
- Forward Checking:
- 기존의 할당(existing assignment)에 추가될 때 제약 조건을 위반(violate)하는 값을 제외(cross off)한다. 이는 변수에 값을 할당할 때마다 해당 값이 다른 변수에 할당된 값과 제약 조건을 위반하는지 확인하는 과정을 의미한다. 만약 위반한다면, 그 값을 해당 변수의 도메인에서 제외한다.
Filtering: Constraint Propagation
Constraint Propagation은 Backtracking 탐색을 개선하기 위한 방법 중 하나로, 제약 조건 간의 상호 작용을 이해하고 활용하여 탐색의 효율성을 높이는 데 도움을 준다.
- Forward Checking은 할당된 변수에서 할당되지 않은 변수로 정보를 전파(propagation)한다. 그러나 모든 실패에 대한 조기 감지(early detection)를 제공하지 않는다.

- NT와 SA는 둘 다 파란색일 수 없다! 이러한 제약 조건을 왜 감지하지 못했을까?
- Constraint Propagation: 제약 조건(constraint)에서 제약 조건(constraint)으로의 추론(reason)이다. 이는 각 제약 조건이 다른 제약 조건에 어떻게 영향을 미치는지를 고려하여 문제의 해결책을 찾는다.
Consistency of A Single Arc
- 일반적인 정의:
- 모든 꼬리(tail)의 x에 대해 어떤 머리(head)의 y가 제약 조건을 위반하지 않고 할당될 수 있으면 화살표(arc) X → Y는 일관성이 있다.(consistent)

- 예시 (Tail = NT, head = WA):
- NT가 파란색인 경우: WA에 빨간색을 할당할 수 있다.
- NT가 녹색인 경우: WA에 빨간색을 할당할 수 있다.
- NT가 빨간색인 경우: WA에 할당할 수 있는 남아있는 할당이 없다.
- 꼬리에서 NT = 빨간색을 삭제하면 이 화살표는 일관성이 있다.
- Forward Checking:
- 각 새로운 할당을 가리키는 화살표(arc)의 일관성(consistency)을 강제한다.(Enforcing)
Arc Consistency of an Entire CSP

- 간단한 형태의 전파(propagation)는 모든 화살표가 일관성이 있도록 한다.
- Arc V to NSW 는 일관성이 있다. : 꼬리에 있는 모든 x에 대해 머리에 있는 어떤 y가 제약 조건을 위반하지 않고 할당될 수 있다.

- Arc SA to NSW 는 일관성이 있다. : 꼬리에 있는 모든 x에 대해 머리에 있는 어떤 y가 제약 조건을 위반하지 않고 할당될 수 있다.

- Arc NSW to SA 는 일관성이 없다. : 만약 NSW에 blue을 할당하면, SA에 할당할 수 있는 유효한 값이 남아있지 않다.
- 이 화살표를 일관성 있게 만들기 위해서는, 꼬리에서 NSW = 파란색을 삭제해야한다.

- Arc V to NSW 로는 일관성이 있었다. 이는 NSW의 도메인에 빨간색과 파란색이 존재 했을 때 였다.
- NSW에서 파란색을 제거한 후, 이 화살표는 더 이상 일관성이 있지 않을 수 있다! 이 화살표를 다시 확인해야 한다.
- 중요한 점: 만약 X가 값을 잃게 되면, X의 이웃들을 다시 확인해야 한다!
- 일관성 있게 만드려면 V의 도메인에서 red를 삭제해야 한다.

- Arc SA to NT 로는 일관성이 없다(inconsistent). : 이를 일관성 있게 만들기 위해 꼬리에서 SA = 파란색을 삭제해야한다.

- Arc SA to NT 로는 일관성이 없다(inconsistent). : 이를 일관성 있게 만들기 위해 꼬리에서 SA = 파란색을 삭제해야한다.
- SA는 빈 도메인을 가지고 있으므로 실패(failure)를 감지(detect)했다. WA = 빨간색 및 Q = 녹색으로 이 CSP를 해결할 방법이 없으므로 backtrack 해야한다.
- Arc Consistency는 Forward Checking보다 더 일찍 실패를 감지한다.
- Arc Consistency는 전처리기(preprocessor)로 실행되거나 각 할당 후(after each assignment)에 실행될 수 있다.
Limitations of Arc Consistency
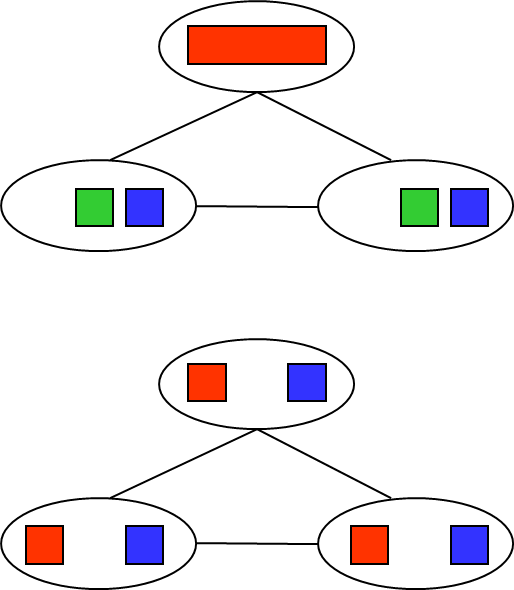
- Arc Consistency 실행 후(after enforcing)의 결과:
- 하나의 해결책이 남아있을 수 있다.
- 여러 해결책이 남아있을 수 있다.
- 해결책이 남아있지 않을 수 있다 (그리고 그것을 모를 수 있다).
- Arc Consistency는 여전히 되돌리기 검색 내(inside a backtracking search)에서 실행된다!
'전공 공부 > 인공지능(Artificial Intelligence)' 카테고리의 다른 글
| [인공지능] CSPs - 5 (0) | 2023.10.15 |
|---|---|
| [인공지능] CSPs- 4 (0) | 2023.10.15 |
| [인공지능] CSPs -2 (2) | 2023.10.15 |
| [인공지능] Constraint Satisfaction Problems - 1 (0) | 2023.10.11 |
| [인공지능] Propositional Logic - 5 (1) | 2023.10.11 |



