Adversarial Search
적대적 검색(Adversarial Search): 제로섬 게임에서 상대적인 움직임을 예측하고, 그에 따라 최적의 움직임을 결정하는 데 사용된다.
Single-Agent Trees

단일 에이전트 트리(Single-Agent Trees):
- 단일 에이전트 트리는 게임에서 하나의 에이전트만이 움직임을 결정하는 상황을 나타낸다. 이러한 트리는 에이전트의 가능한 모든 움직임과 그에 따른 결과를 나타낸다.
- 이러한 트리는 에이전트가 최적의 움직임을 결정하기 위해 사용된다. 각 노드는 특정 상태를 나타내며, 에이전트는 이 트리를 사용하여 최적의 움직임을 결정할 수 있다.
- 단일 에이전트 트리는 게임의 각 단계에서 에이전트가 취할 수 있는 모든 가능한 움직임을 나타내는 노드로 구성된다. 각 노드는 그 움직임의 결과를 나타내는 자식 노드를 가질 수 있다.
- 밑에 숫자는 무엇인지 찾아 볼것
Value of a State

- 상태의 가치(Value of a State):
- 상태의 가치는 해당 상태에서 달성 가능한 최상의 결과(유틸리티)를 의미한다.
- 비종료 상태(Non-Terminal States):
- 게임이 아직 종료되지 않은 상태를 의미한다. 이러한 상태에서는 에이전트가 다양한 움직임을 선택할 수 있으며, 각 움직임은 다른 결과를 초래할 수 있다.

- 종료 상태(Terminal States):
- 게임이 종료된 상태를 의미한다. 종료 상태에서는 더 이상 움직일 수 있는 선택지가 없으며, 각 플레이어에게 주어진 유틸리티 값이 결정된다.

Adversarial Game Trees

적대적 게임 트리(Adversarial Game Trees):
- 적대적 게임 트리는 두 에이전트가 게임을 플레이할 때 각 상태에서의 가능한 움직임과 그에 따른 결과를 나타내는 트리 구조이다.
- 이러한 트리는 각 노드에서의 최적의 움직임을 결정하기 위해 사용된다. 각 노드는 특정 상태를 나타내며, 에이전트는 이 트리를 사용하여 상대방의 움직임에 대응하는 자신의 최적의 움직임을 결정할 수 있다.
- 적대적 게임 트리는 게임의 각 단계에서 에이전트가 취할 수 있는 모든 가능한 움직임을 나타내는 노드로 구성된다. 각 노드는 그 움직임의 결과를 나타내는 자식 노드를 가질 수 있다.
- 밑에 점수는 무엇인지 찾아볼 것
Minimax Values

- 에이전트의 제어 하에 있는 상태(States Under Agent’s Control):
- 에이전트가 현재 상태에서 취할 수 있는 모든 가능한 움직임 중에서 최적의 움직임을 결정하는 상태를 의미한다. 이러한 상태에서 에이전트는 결과를 최대화하기 위해 움직임을 선택한다.

- 상대방의 제어 하에 있는 상태(States Under Opponent’s Control):
- 상대방이 현재 상태에서 취할 수 있는 모든 가능한 움직임 중에서 최적의 움직임을 결정하는 상태를 의미한다. 이러한 상태에서 상대방은 에이전트의 결과를 최소화하기 위해 움직임을 선택한다.

- 종료 상태(Terminal States):
- 게임이 종료된 상태를 의미한다. 종료 상태에서는 더 이상 움직일 수 있는 선택지가 없으며, 각 플레이어에게 주어진 유틸리티 값이 결정된다.

Tic-Tac-Toe Game Tree

Tic-Tac-Toe 게임 트리(Tic-Tac-Toe Game Tree):
- Tic-Tac-Toe는 결정론적이며 제로섬 게임이다. 예를 들어, 틱택토, 체스, 체커와 같은 게임들이 이에 해당한다.
- 한 플레이어는 결과를 최대화하려고 하며, 다른 플레이어는 결과를 최소화하려고 한다.
- Minimax 검색은 상태 공간 검색 트리를 사용합니다. 플레이어들은 번갈아 가며 턴을 진행한다.
- 각 노드의 minimax 값은 최적의 상대방에 대한 최상의 달성 가능한 유틸리티를 계산하기 위해 재귀적으로 계산된다. 이 값은 게임의 일부로 제공되는 종료 값과는 다르다
- 인터넷 검색 해볼 것
Adversarial Search (Minimax)

- 결정론적, 제로섬 게임(Deterministic, Zero-Sum Games):
- 예로는 틱택토(Tic-tac-toe), 체스(Chess), 체커(Checkers) 등이 있다.
- 한 플레이어는 결과를 최대화하려고 한다.
- 다른 플레이어는 결과를 최소화하려고 한다.
- Minimax 검색(Minimax Search):
- 상태 공간 검색 트리(State-Space Search Tree)를 사용한다.
- 플레이어들은 번갈아 가며 턴을 진행한다.
- 각 노드의 minimax 값을 계산한다 : 합리적인 최적의 상대방(rational optimal adversary)에 대한 최상의 달성 가능한 유틸리티(best achievable utility)를 계산한다.
minimax values : 재귀적으로 계산
terminal value: 게임의 일부분
Minimax Implementation
이 코드들은 Minimax 알고리즘의 기본 구현을 나타낸다.
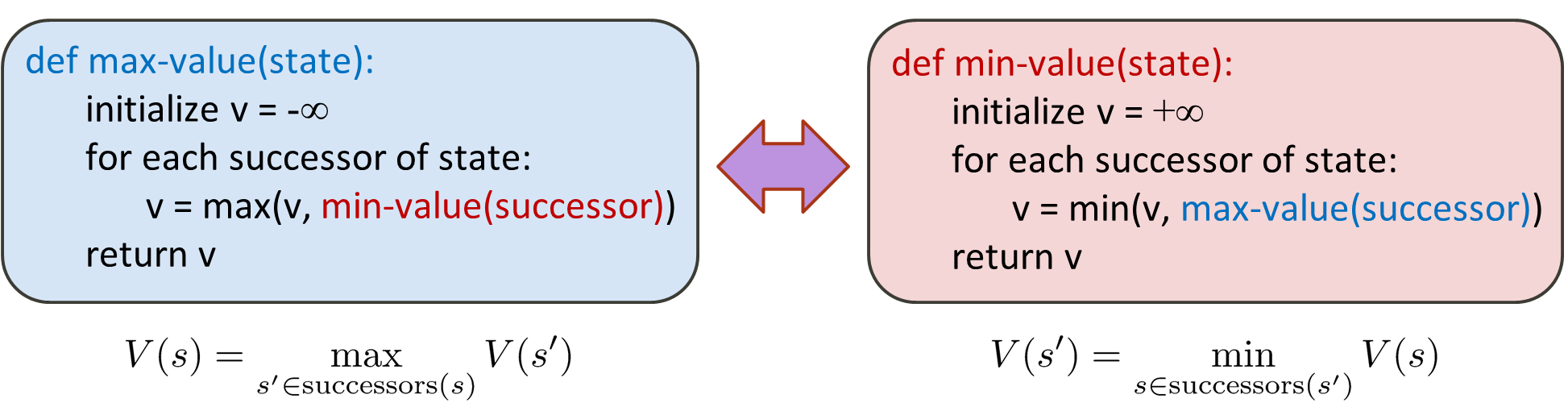
def max-value(state):
initialize v = -∞
for each successor of state:
v = max(v, min-value(successor))
return v
max-value 함수:
- 이 함수는 주어진 상태에서 가능한 모든 후속 상태를 고려하여 최대 유틸리티 값을 계산한다.
- 초기값 v는 -∞로 설정된다. 이는 최대 값을 찾기 위한 시작점으로 사용된다.
- 각 후속 상태에 대해 min-value 함수를 호출하여 해당 상태의 최소 값을 얻는다. 그리고 그 값을 현재의 v 값과 비교하여 더 큰 값을 v에 저장한다.
- 모든 후속 상태를 고려한 후, 최종적으로 계산된 v 값을 반환한다.

def min-value(state):
initialize v = +∞
for each successor of state:
v = min(v, max-value(successor))
return v
min-value 함수:
- 이 함수는 주어진 상태에서 가능한 모든 후속 상태를 고려하여 최소 유틸리티 값을 계산한다.
- 초기값 v는 +∞로 설정된다. 이는 최소 값을 찾기 위한 시작점으로 사용된다.
- 각 후속 상태에 대해 max-value 함수를 호출하여 해당 상태의 최대 값을 얻는다. 그리고 그 값을 현재의 v 값과 비교하여 더 작은 값을 v에 저장한다.
- 모든 후속 상태를 고려한 후, 최종적으로 계산된 v 값을 반환한다.

Minimax Implementation (Dispatch)

def value(state):
if the state is a terminal state: return the state’s utility
if the next agent is MAX: return max-value(state)
if the next agent is MIN: return min-value(state)
value 함수:
- 이 함수는 주어진 상태의 값을 계산한다.
- 만약 주어진 상태가 종료 상태(terminal state)라면, 해당 상태의 유틸리티(utility) 값을 반환한다.
- 다음 에이전트가 MAX라면, max-value 함수를 호출하여 해당 상태의 최대 값을 반환한다.
- 다음 에이전트가 MIN이라면, min-value 함수를 호출하여 해당 상태의 최소 값을 반환한다.
Minimax Example
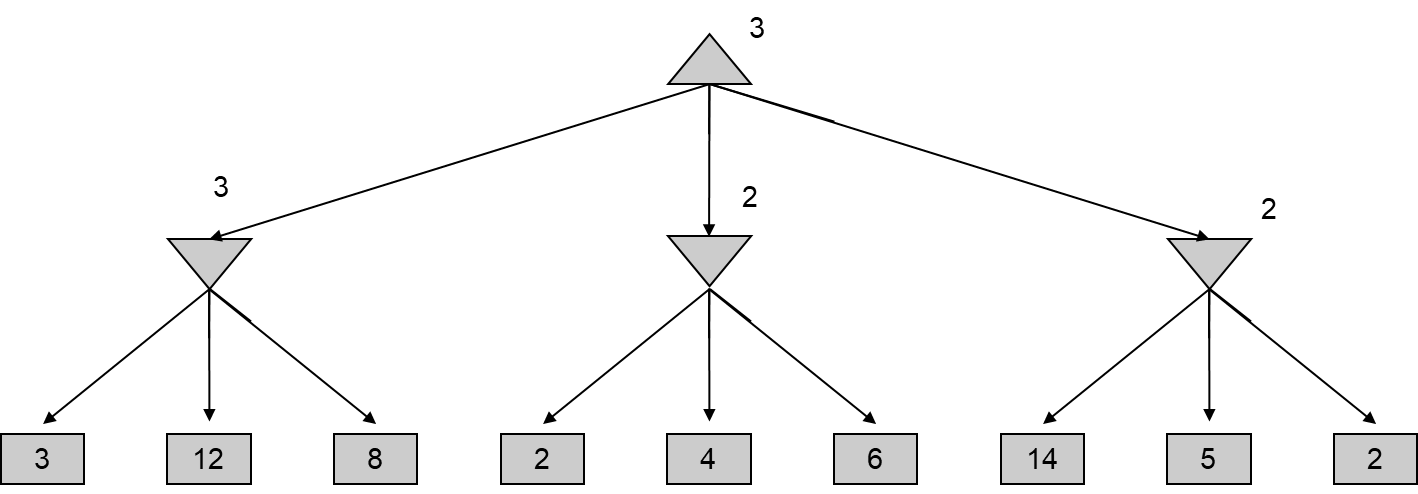
Minimax 예제:
- 트리의 각 노드는 게임의 특정 상태를 나타낸다. 노드의 값은 해당 상태에서의 유틸리티(게임 결과)를 나타낸다.
- 트리의 노드는 MAX 또는 MIN 에이전트에 의해 제어된다. MAX 에이전트는 결과를 최대화하려고 하며, MIN 에이전트는 결과를 최소화하려고 한다.
- 예제 트리에서는 다양한 상태와 그에 따른 유틸리티 값들이 표시되어 있다. 예를 들어, 값이 3, 12, 8, 2, 4, 6, 14, 5, 2인 노드들이 있다.
Minimax Properties
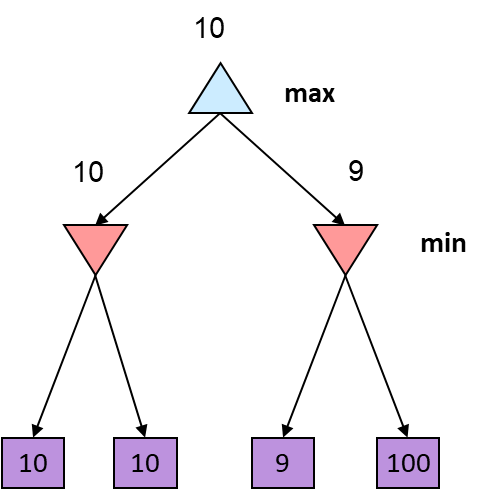
Minimax 특성 : Optimal against a perfect player. Otherwise?
- Minimax 알고리즘은 완벽한 플레이어(즉, 항상 최적의 움직임을 하는 플레이어)에 대해 최적이다. 이는 Minimax 알고리즘이 게임 트리의 모든 가능한 움직임을 고려하므로, 완벽한 플레이어에 대해 항상 최적의 움직임을 찾을 수 있음을 의미한다.
- 그렇다면 완벽하지 않은 플레이어, 즉 실수를 하는 플레이어에 대해서는 어떨까? 이 경우 Minimax 알고리즘은 여전히 최적의 움직임을 찾을 수 있지만, 실제 게임에서 상대방이 예상치 못한 움직임을 할 수도 있다. 따라서 실제 게임에서는 Minimax 알고리즘만으로는 항상 승리할 수 없을 수도 있다.
Minimax Efficiency
Minimax의 효율성(Efficiency)은 어떻게 되는가?
- Minimax는 (완전 Exhaustive) Depth-First Search(DFS)과 유사하다.
- 시간 복잡도(Time Complexity):
- 여기서 는 각 상태에서의 가능한 움직임의 수(분기 계수)이며, 은 게임 트리의 최대 깊이이다.
- 공간 복잡도(Space Complexity):
- 예시: 체스의 경우 ( b » 35, m » 100)
- 체스에서 각 상태에서의 가능한 움직임의 수 는 대략 35이며, 게임 트리의 최대 깊이 는 대략 100이다.
- 이러한 매개변수로는 정확한(exact) 해결책을 찾는 것이 완전히 불가능하다(completely infeasible). 이는 게임 트리의 크기가 매우 크기 때문이다.
- 그러나, 전체 게임 트리를 탐색할 필요가 있을까? 실제로는 전체 트리를 탐색하지 않고도 효율적인 움직임을 찾을 수 있는 방법들이 있다.
- 체스에서 각 상태에서의 가능한 움직임의 수 는 대략 35이며, 게임 트리의 최대 깊이 는 대략 100이다.
'전공 공부 > 인공지능(Artificial Intelligence)' 카테고리의 다른 글
| [인공지능] Adversarial Search 1 - 4 (0) | 2023.10.16 |
|---|---|
| [인공지능] Adversarial Search 1 - 3 (0) | 2023.10.16 |
| [인공지능] Adversarial Search 1 - 1 (0) | 2023.10.16 |
| [인공지능] CSPs - 5 (0) | 2023.10.15 |
| [인공지능] CSPs- 4 (0) | 2023.10.15 |



