Regular expression and finite automata
How can we represent regular expressions in finite automata?
RE를 FA에서 어떻게 표현할 수 있는가?
- 𝐿(𝑎* + 𝑎* (𝑎 + 𝑏) 𝑐* )

- 첫번째 방법 : 일반화된(Generalized) NFA , 통칭 ,GTG( Generalized Transition Graph ) 사용
- 기본적인 NFA는 전이(transition)를 나타내는 라벨로 알파벳 Σ의 구성원만을 사용합니다. 그러나 일반화된 NFA (또는 GTG)는 전이를 나타내는 라벨로 정규 표현식(Regular expressions)을 사용합니다. 이렇게 함으로써, 각 전이가 단순한 문자 대신 더 복잡한 문자열 패턴을 나타낼 수 있게 됩니다.
- 예를 들어, 기본 NFA에서는 상태 A에서 상태 B로의 전이가 'a' 또는 'b' 문자에 의해 발생한다면, 두 개의 별도의 전이가 필요합니다. 그러나 GTG에서는 단일 전이에 'a+b'와 같은 정규 표현식 라벨을 사용하여 동일한 동작을 나타낼 수 있습니다.

- 정규 표현식을 규칙(rule)에 따라 분할(Spilit)하는 방법:
- UNION 연산(operation)

이 그래프는 밑의 transition graph와 동일하다.

- CONCATENATION(결합) 연산(operation)

이 그래프는 밑의 transition graph와 동일하다.

- STAR 연산(operation)
- CASE 1) 왼쪽 끝 상태(left-most state)에서 나가는 화살표(outgoing edge)가 하나만 있는 경우
- 이 경우, 해당 상태에서 자기 자신으로 돌아가는 루프(반복 전이)를 추가하여 STAR 연산을 표현할 수 있습니다.
- CASE 1) 왼쪽 끝 상태(left-most state)에서 나가는 화살표(outgoing edge)가 하나만 있는 경우

이 그래프는 밑의 그래프와 동일하다.

- STAR 연산(operation)
- CASE 2) 오른쪽 끝 상태(right-most state)에서 들어오는 화살표(incoming edge)가 하나만 있는 경우
- 이 경우, 해당 상태에서 시작 상태로 돌아가는 전이를 추가하여 STAR 연산을 표현할 수 있습니다.
- CASE 2) 오른쪽 끝 상태(right-most state)에서 들어오는 화살표(incoming edge)가 하나만 있는 경우

위 그래프는 밑의 그래프와 같다.
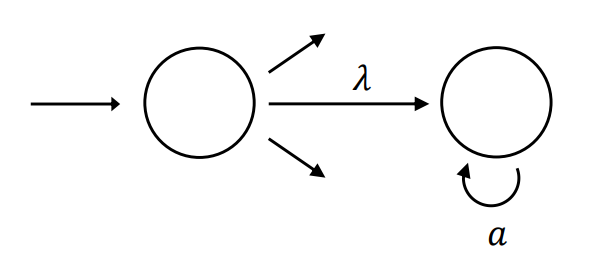
- STAR 연산(operation)
- CASE 3) 나머지 경우 (Remaing Cases)
- 새로운 상태 생성 (generating a new state)
- CASE 3) 나머지 경우 (Remaing Cases)
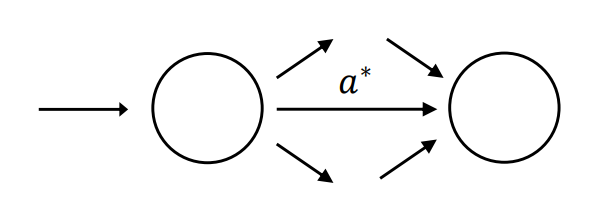
일반적으로 새로운 시작 상태와 종료 상태를 생성하고, 이 두 상태 사이에 원래 NFA를 배치합니다. 새로운 시작 상태에서 원래 NFA의 시작 상태로, 그리고 원래 NFA의 종료 상태에서 새로운 종료 상태로 전이를 추가합니다. 또한, 새로운 시작 상태에서 새로운 종료 상태로 직접 전이를 추가하여 0번의 반복(즉, 빈 문자열)도 수용하도록 합니다.

예제 문제
- 𝑟 = (𝑎𝑏 +𝑏𝑎)*

이 그래프는 아래 그래프와 같다

ab는 아래와 같이 표현할 수 있다.

ba도 아래와 같이 표현할 수 있다. 최종 그래프는 다음과 같다.

- 10 + (0 +11) 0*1
정규 표현식으로 아래 그래프와 같이 기본적인 그래프 표현이 가능하다

이 그래프는 아래 그래프와 같이 표현할 수 있다
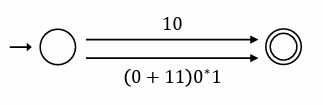
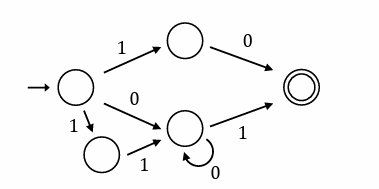
CONCATION 결합으로 이루어진 각각의 연산을 분해하여 새로운 상태로 만들어 다음과 같이 표현할 수 있다.

스타 연산은 반복 연산으로 표현하여 다음과 같이 표현할 수 있다

UNION 연산도 풀어 표현하여 최종 그래프는 다음과 같다.
실습 문제
- (𝑎 +𝑏)*𝑎𝑏*𝑎(𝑎 +𝑏𝑎)*