[계산이론] Regular Languages and Regular Grammars - 4

Regular Grammars

정규 문법은 특정(certain) 형태의 생성 규칙을 사용하여 정규 언어를 정의합니다.

• 오른쪽 선형 (Right-Linear) grammars 과 왼쪽 선형 (Left-Linear) grammars
  • 문법 G = (V, T, S, P)는 모든 생성 규칙이 다음 형태를 가질 때 오른쪽 선형  (Right-Linear)  이라고 합니다:
    • 𝐴→𝑥𝐵
    • 𝐴→𝑥
    • 여기서 𝐴와 𝐵는 변수 V의 원소 (𝐴,𝐵 ∈ 𝑉)  이며, 𝑥는 터미널 문자열 T의 원소 ( 𝑥 ∈ 𝑇* )입니다. 
  • 문법 G = (V, T, S, P)는 모든 생성 규칙이 다음 형태를 가질 때 왼쪽 선형 (Left-Linear)  이라고 합니다:
    • 𝐴→𝐵𝑥
    • 𝐴→𝑥
    • 여기서도 𝐴와 𝐵는 변수이며, 𝑥는 터미널 문자열입니다.
•   정규 문법은 오른쪽 선형 또는 왼쪽 선형 중 하나입니다.
  • 즉, 생성 규칙이 오른쪽 선형 또는 왼쪽 선형 형태만을 가질 때 해당 문법은 정규 문법이라고 합니다.
• 오른쪽 선형 (Right-Linear)
  • 예: 문법 𝐺1 = ({𝑆} , {𝑎, 𝑏} ,𝑆,𝑃1)
    • 𝑃1 is given as: 𝑆 → 𝑎𝑏𝑆 | 𝑎
  • 이 문법은 오른쪽 선형입니다. 생성 규칙은 변수 𝑆가 터미널 문자열 𝑎𝑏와 다른 변수 𝑆로 대체되거나, 터미널 문자열 𝑎로만 대체되는 형태를 가집니다.
•  왼쪽 선형 (Left-Linear)
  • 예: 문법 𝐺2 = ({𝑆} , {𝑎, 𝑏} ,𝑆,𝑃2)
    • 𝑃2 is given as : 𝑆 → 𝑆𝑎𝑏 | 𝑏
  • 이 문법은 왼쪽 선형입니다. 생성 규칙은 변수 𝑆가 다른 변수 𝑆와 터미널 문자열 𝑎𝑏로 대체되거나, 터미널 문자열 𝑏로만 대체되는 형태를 가집니다.
•  정규 문법이 아닌 경우
  • 예: 문법 𝐺3 = ({𝑆, 𝐴,𝐵} , {𝑎, 𝑏} ,𝑆,𝑃3)
    • 𝑃3 is given as:
      • 𝑆→𝐴
      • 𝐴→𝑎𝐵|𝜆
      • 𝐵→𝐴𝑏
  • 이 문법은 정규 문법이 아닙니다. 생성 규칙 중 𝐵→𝐴𝑏는 오른쪽 선형도 왼쪽 선형도 아닌 형태를 가지므로, 이 문법은 정규 문법이 아닙니다.

정규 문법에서 유한 오토마타로의 변환( Regular grammars to finite automata )

 

• 𝐺 = ({ 𝑆, 𝐴} , {𝑎, 𝑏} ,𝑆,𝑃)를 가지는 언어 L(G) 와 생성 규칙 𝑃를 기반으로 유한 오토마타를 구성해라
  • P is given as 
    • 𝑆→𝑎𝑆 | 𝑏𝐴 | 𝑏
    • 𝐴→𝑎𝐴 | 𝑏𝑆  |𝑎

1. 각 생성 규칙(production) 𝐴𝑖 → 𝑎𝐴𝑗는 상태 𝑞𝑖에서 상태 𝑞𝑗로의 label 𝑎를 가진 전이(transition)를 유도합니다.(induce)
2. 각 생성 규칙 𝐴𝑘 → 𝑎는 상태 𝑞𝑘에서 (종료) 상태 𝑞𝑓로의 label 𝑎를 가진 전이(transition)를 유도합니다.(induce)

이러한 방식으로 구성된 transition 그래프는 다음과 같다.

 

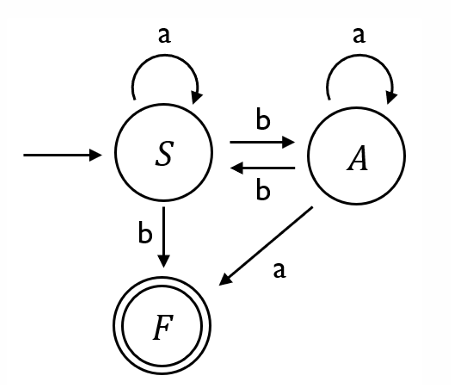
실습문제

• Construct a finite automaton recognizing 𝐿(𝐺) where 𝐺 = ({𝑆, 𝐴} , {𝑎, 𝑏} ,𝑆, 𝑃 )with 𝑃 given as
  • 𝑆→𝑎𝑆
  • 𝐴→𝑏𝐵
  • 𝐵→𝑎𝐶
  • 𝐶→ 𝑎

유한 오토마타 (DFA)에서 정규 문법으로의 변환 ( DFA to regular grammar )

• Construct a regular grammar from given DFA ( 주어진 DFA으로 정규 문법을 구성해라)
  • 𝐴𝑖 →𝑎𝐴𝑗 constructed if (𝑞𝑖,𝑎) = 𝑞𝑗 where 𝑞𝑗 ∉ 𝐹
  • 𝐴𝑖 →𝑎𝐴𝑗 and 𝐴𝑖 → 𝑎 constructed if (𝑞𝑖,𝑎) = 𝑞𝑗 where 𝑞𝑗 ∈  𝐹

만약 DFA에서 상태 𝑞𝑖에서 label 𝑎를 통해 상태 𝑞𝑗로 전이(transition)가 있고, 𝑞𝑗가 수락 상태가 아니라면, 생성 규칙 𝐴𝑖 →𝑎𝐴𝑗를 정규 문법에 추가합니다.

만약 DFA에서 상태 𝑞𝑖에서 label 𝑎를 통해 상태 𝑞𝑗로 전이가 있고, 𝑞𝑗가 수락 상태라면, 두 가지 생성 규칙 𝐴𝑖 →𝑎𝐴𝑗와 𝐴𝑖 → 𝑎 을 정규 문법에 추가합니다.

 

=====>

 

만들어진 Grammar

 

• 𝐺=(𝑉,𝑇,𝑃,𝑆)
  • 𝑉= {  𝑆, 𝐴  }
  • 𝑇= { 𝑎, 𝑏  }
  • 𝑃
    • 𝑆 →𝑎𝑆 | 𝑏𝐴 | 𝑏 
    • 𝐴 →𝑎𝐴 | 𝑏𝐴 | 𝑎 | 𝑏

Description of regular language

정규 언어의 설명

정규 언어는 RE , DFA/NFA , RG로 표현될 수 있는데

다음 그림과 같이 표현 방법끼리 서로 변환하여 표현할 수 있다.