렉쳐 3 실습 문제
- 주어진 정규 표현식에 대한 DFA(결정적 유한 오토마타)를 찾고, 그 후 정규 문법을 추출하라.
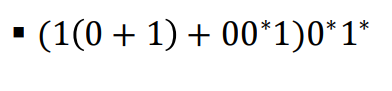
Closure properties of regular languages ( 정규 언어의 폐포 속성)
정규 언어에 연산(operation)을 수행하면 어떤 일이 발생하는가
- 예를 들어, 두 정규 언어 𝐿1과 𝐿2가 주어졌을 때: 그들의 합집합도 정규인가?"
- "예
- 정규 언어는 합집합(union)에 대해 폐쇄(closed)되어 있다.
- 만약 𝐿1과 𝐿2가 정규 언어라면, 아래도 모두 정규 언어이다:

만약 𝑳1과 𝑳2가 정규 언어라면, 𝑳1 ∪ 𝑳2도 그렇다.
- 𝑟1과 𝑟2는 정규 표현식이라고 가정하면, 𝐿 𝑟1 = 𝐿1 그리고 𝐿 𝑟2 = 𝐿2 이다.
- 𝐿 𝑟1 ∪ 𝐿 𝑟2 = 𝐿(𝑟1 + 𝑟2) 임을 주목하라.
- 여기서, 𝑟1 + 𝑟2는 정규 표현식이다.
- 따라서, 𝐿1 ∪ 𝐿2는 정규 언어이다.

만약 𝑳1과 𝑳2가 정규 언어라면, 𝑳1 ∙ 𝑳2도 그렇다.
- 𝑟1과 𝑟2는 𝐿 𝑟1 = 𝐿1 그리고 𝐿 𝑟2 = 𝐿2 인 정규 표현식이라 가정하자.
- 𝐿 𝑟1 ∙ 𝐿 𝑟2 = 𝐿(𝑟1 ∙ 𝑟2) 임을 주목하라.
- 여기서, 𝑟1 ∙ 𝑟2는 정규 표현식이다.
- 따라서, 𝐿1 ∙ 𝐿2는 정규 언어이다.

만약 𝑳1이 정규 언어라면, 𝑳1* 도 그렇다.
- 𝐿 (𝑟1) = 𝐿1 인 정규 표현식이 𝑟1이라고 가정하자.
- (𝐿 (𝑟1))* = 𝐿(𝑟1*) 임을 주목하라.
- 여기서, 𝑟1* 는 정규 표현식이다.
- 따라서, 𝐿1* 는 정규 언어이다.

만약 𝑳1이 정규 언어라면, 𝑳1bar도 그렇다.
- 𝐿1bar을 수용하는 DFA Mbar를 어떻게 생성할까요?
- 다음과 같은 DFA 𝑀을 고려하라: 𝐿 (𝑀)={ 𝑤11| 𝑤 ∈ {0, 1}* }
- ❖ 𝐿 (Mbar) 를 수용할 수 있는 DFA Mbar는 다음과 같이 구성됩니다.



- 𝐿1을 수용하는 DFA 𝑀 = (𝑄, Σ, 𝛿, 𝑞0, 𝐹)를 고려하라.
- 우리는 𝐿1을bar 수용하는 DFA 𝑀bar= (𝑄, Σ, 𝛿, 𝑞0, 𝑸 − 𝑭)를 구성할 수 있다.
- 따라서, 𝐿1bar는 정규 언어이다.
만약 𝑳1과 𝑳2가 정규 언어라면, 𝑳1 ∩ 𝑳2도 그렇다.
- 드모르간의 법칙을 사용
- 𝐴 ∪ 𝐵 = 𝐴ҧ∩ 𝐵ത
- 𝐴 ∩ 𝐵 = 𝐴ҧ∪ 𝐵ത
- 𝐿1 ∩ 𝐿2 = (𝐿1 ∪ 𝐿2)
- 만약 𝐿1과 𝐿2가 정규 언어라면, 𝐿1과 𝐿2도 그렇다.
- 만약 𝐿1과 𝐿2가 정규 언어라면, 𝐿1 ∪ 𝐿2도 그렇다.
- 만약 𝐿1 ∪ 𝐿2가 정규 언어라면, (𝐿1 ∪ 𝐿2)도 그렇다.
- 따라서, 𝐿1 ∩ 𝐿2는 정규 언어이다.

만약 𝑳1과 𝑳2가 정규 언어라면, 𝑳1 − 𝑳2도 그렇다.
- 다음 사실을 사용할 수 있다.
- 𝐿1 − 𝐿2 = 𝐿1 ∩ 𝐿2bar
- 따라서, 𝐿1 − 𝐿2는 정규 언어이다.
