Lecture3 실습문제
- 주어진 정규 표현식에 대한 DFA를 찾고, 그 후에 정규 문법을 추출하라.

solution


Identifying non-regular languages ( 정규 아닌 언어 파악하기)
정규 아닌 언어들
- 정규 아닌 언어들은 유한 오토마타로 인식될 수 없다.
- 주장: 𝐿 = 0^𝑛1^𝑛 (𝑛 ≥ 0)은 정규가 아니다.
- 이 정규 언어라면 L에 대한 DFA를 구성할 수 있어야 한다.
- 그러나 DFA는 제한된 임시 저장 공간을 가지고 있으므로 n를 기억할 수 없다.

비둘기집 원칙
- 만약 𝑛마리의 비둘기가 𝑚개의 비둘기집에 위치한다면,
- 하나의 비둘기집에는 적어도 𝑛/𝑚마리의 비둘기가 있을 것이다.
- 만약 우리가 𝑛개의 물체를 𝑚개의 상자에 넣고 𝑛 > 𝑚이면, 적어도 하나의 상자는 그 안에 두 개 이상의 물체를 가져야 한다.
정규 아닌 언어를 파악하는 기본 아이디어
- 𝑛개의 상태를 가진 유한 오토마타를 고려하라.
- 𝑚이라는 길이의 입력 문자열이 주어지고 여기서 𝑚 > 𝑛일 때,
- 그러면 하나 또는 그 이상의 상태들은 반드시 여러 번 방문될 것이다.
펌핑 레마( Pumping lemma)
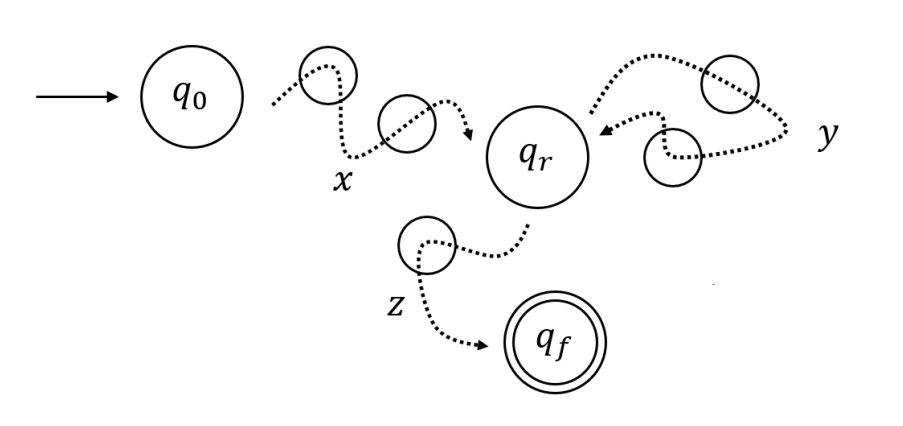

- 𝐿이 정규 언어라고 하자.
- 양의 정수 𝑚이 존재하여, 𝑤 ∈ 𝐿인 모든 𝑤에 대하여, 만약 𝑤의 길이가 𝑚 이상이면, 다음을 만족하는 𝑤 = 𝑥𝑦𝑧가 존재한다.
- 𝑥𝑦의 길이는 𝑚 이하
- 𝑦의 길이는 1 이상
- 모든 𝑖에 대하여 𝑖 ≥ 0일 때, 𝑥𝑦^𝑖𝑧는 𝐿에 속한다.
- 충분히 긴 길이의 문자열 (|𝑤| ≥ 𝑚)은 𝑥𝑦𝑧 형태로 표현될 수 있으며, "𝑦"를 𝑖번 펌핑한 𝑥𝑦^𝑖𝑧는 또한 항상 이 언어에 속할 수 있다.

펌핑 레마의 증명
- 𝐿이 정규 언어라면, 그것을 인식하는 DFA 𝑀 = (𝑄, Σ, 𝛿, 𝑞0, 𝐹)이 존재한다.
- 𝑄를 𝑛 + 1이라 하자 (𝑀은 𝑞0, 𝑞1, … , 𝑞𝑛으로 라벨링된 상태를 가진다).
- 𝑤 ∈ 𝐿인 문자열을 가져오되, 𝑤의 길이는 𝑚 = 𝑛 + 1 이상이어야 한다.
- 𝑤를 처리하면서 𝑀이 통과하는 상태 집합을 고려하자: 𝑞0, 𝑞𝑖, 𝑞𝑗, … , 𝑞𝑓.
- 이 순서에는 𝑤 + 1 상태가 있으므로, 적어도 하나의 상태는 반복되어야 한다.
- 이러한 반복은 𝑛번째 움직임 이후에 시작되어야 한다.
- 예: 𝑞0, 𝑞𝑖, 𝑞𝑗, … , 𝑞𝑟, … , 𝑞𝑟, … , 𝑞𝑓
- 이것은 𝑤의 부분 문자열 𝑥, 𝑦, 𝑧가 있어야 함을 나타낸다.
- 𝛿∗(𝑞0, 𝑥) = 𝑞𝑟, 𝛿∗(𝑞𝑟, 𝑦) = 𝑞𝑟, 𝛿∗(𝑞𝑟, 𝑧) = 𝑞𝑓 (여기서 𝑥𝑦의 길이는 𝑛 + 1 이하이고 𝑦의 길이는 1 이상이다.)
- 이로부터, 다음 조건들이 만족된다.
- 𝛿∗(𝑞0, 𝑥𝑧) = 𝑞𝑓, 𝛿∗(𝑞0, 𝑥𝑦^2𝑧) = 𝑞𝑓, 𝛿∗(𝑞0, 𝑥𝑦^3𝑧) = 𝑞𝑓, 𝛿∗(𝑞0, 𝑥𝑦^𝑖𝑧) = 𝑞𝑓.

펌핑 레마( Pumping lemma)
- 𝐿 = 𝑎^𝑛𝑏^𝑛, 𝑛 ≥ 0 이 정규 언어가 아니라는 것을 보여라.
- 𝐿이 정규 언어라고 가정하면, 펌핑 레마는 반드시 성립해야 한다.
- 𝑚을 𝑛이라 하자.
- 𝑥𝑦 ≤ 𝑚이기 때문에, 부분 문자열 𝑦는 전적으로 𝑎로만 구성되어야 한다(𝑦 = 𝑘라고 가정하자).
- 𝑖 = 0일 때, 𝑤0 = 𝑎^(𝑚−𝑘)𝑏^𝑚 이다.
- 𝑎^(𝑚−𝑘)𝑏^𝑚 는 명백하게 𝐿에 포함되지 않는다 => 𝐿은 정규 언어가 아니다.

- Σ = 𝑎, 𝑏 일 때, 𝐿 = 𝑤𝑤𝑅 : 𝑤 ∈ Σ^∗ 가 정규 언어가 아니라는 것을 보여라.
- 𝐿이 정규 언어라고 가정하면, 펌핑 레마는 반드시 성립해야 한다.
- 양의 정수 𝑚을 고려하고, 𝑤′ = 𝑤𝑤𝑅 을 𝑎^𝑚𝑏^𝑚𝑏^𝑚𝑎^𝑚 이라 하자.
- 𝑥𝑦 ≤ 𝑚 이기 때문에, 부분 문자열 𝑦는 전적으로 𝑎로만 구성되어야 한다(𝑦 = 𝑘라고 가정하자).
- 𝑖 = 0일 때, 𝑤′ = 𝑎^(𝑚−𝑘)𝑏^𝑚𝑏^𝑚𝑎^𝑚 (𝐿에 포함되지 않음)
- 𝐿은 정규 언어가 아니다.

- 펌핑 레마가 위반됨 => 정규 언어가 아니다.
- 펌핑 레마가 위반되지 않음 => 정규 언어인지 아닌지 알 수 없다.
- Σ = 𝑎, 𝑏 일 때, 𝐿 = 𝑤 ∈ Σ^∗ : 𝑛𝑎(𝑤) < 𝑛𝑏(𝑤) 가 정규 언어가 아님을 보여라.
- 𝐿이 정규 언어라고 가정하면, 펌핑 레마가 성립해야 한다.
- 양의 정수 𝑚을 고려하고 𝑤 = 𝑎^𝑚𝑏^𝑚+1 라 하자.
- 𝑥𝑦 ≤ 𝑚 이므로, 부분 문자열 𝑦는 전적으로 𝑎로 이루어져야 한다 (𝑦 = 𝑘 ≥ 1 이라고 가정하자).
- 𝑖 = 2 일 때, 𝑤 = 𝑎^𝑚+𝑘𝑏^𝑚+1 이 되며 (𝐿에 속하지 않는다).
- 따라서, 𝐿은 정규 언어가 아니다.
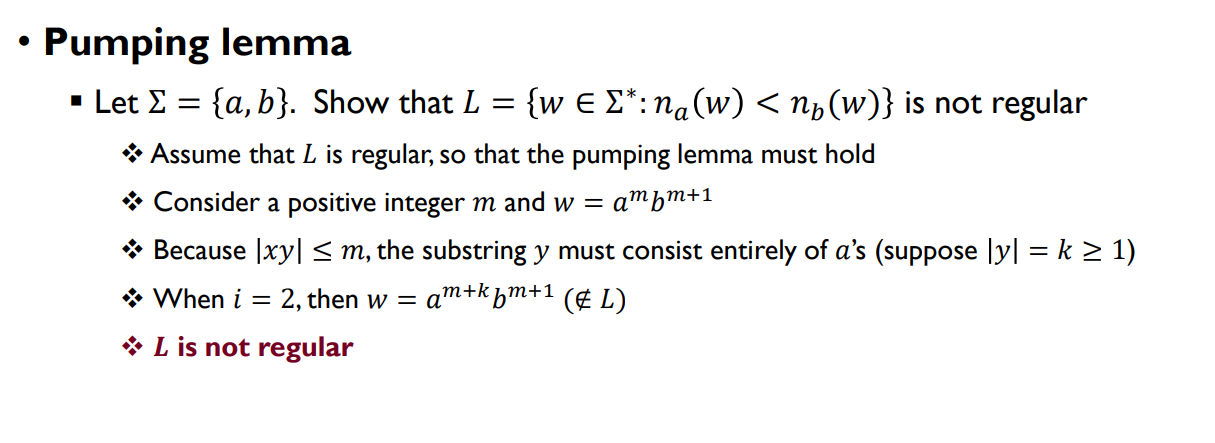
- Σ = 𝑎, 𝑏 일 때, 𝐿 = 𝑤𝑤|𝑤 ∈ Σ^∗ 가 정규 언어가 아님을 보여라.
- 𝐿이 정규 언어라고 가정하면, 펌핑 레마가 성립해야 한다.
- 양의 정수 𝑚을 고려하고 𝑤 = 𝑎^𝑚𝑏𝑎^𝑚𝑏 라 하자.
- 𝑥𝑦 ≤ 𝑚 이므로, 부분 문자열 𝑦는 전적으로 𝑎로 이루어져야 한다 (𝑦 = 𝑘 ≥ 1 이라고 가정하자).
- 𝑖 = 0 일 때, 𝑤 = 𝑎^𝑚−𝑘𝑏𝑎^𝑚𝑏 가 되며 (𝐿에 속하지 않는다).
- 따라서, 𝐿은 정규 언어가 아니다.
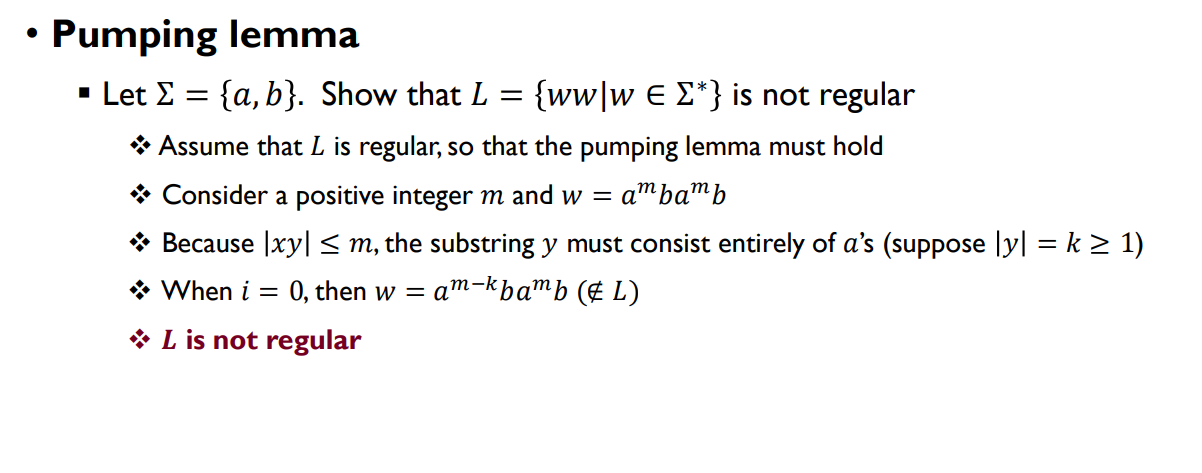
펌핑 레마 : 실습 문제
- ▪ 𝐿 = 𝑎^𝑖𝑏^𝑗𝑐^𝑘 에 대해, 𝑖 + 𝑗 ≤ 𝑘 일 때, 𝐿이 정규 언어가 아님을 보여라.

▪ 𝐿 = 0^𝑛^2 에 대해, 𝑛 ≥ 0 일 때, 𝐿이 정규 언어가 아님을 보여라.
