두 가지 가능한 (가상의hypothetical) 세계 – 왜 가상의일까?
(상상할 수 있는) P의 두 가지 "버전"? A가 무엇인지에 따라 우리는 이러한 세계에 살고 있을 수도, 살고 있지 않을 수도 있습니다!

주의하십시오. P^는 "A가 P 안에 있다면 P는 어떤 모습이 될까?"라는 클래스와 동일하지 않습니다. 이 P의 두 가지 버전은 두 가지 다른 가능한 세계에 해당합니다. 첫 번째 세계에서, 우리의 프로그래밍 언어는 어떤 A의 인스턴스도 단 한 단계로 해결할 수 있는 마법 같은 새로운 명령어로 확장됩니다. 그러나, 이 명령어가 어떻게 작동하는지 우리는 알 수 없습니다. 오라클의 생각 과정을 볼 수 없기 때문입니다. 두 번째 세계에서는, A가 P 안에 있을 때, 다항 시간 안에 A를 해결하는 프로그램이 있습니다. 이 프로그램은 우리의 프로그래밍 언어의 일반적인 명령어만을 사용하여 작성됩니다. 이는 우리가 이해하고 원하는 대로 수정할 수 있는 다른 어떤 프로그램과도 같습니다.
- "두 가지 가능한 (가상의) 세계"는 어떤 문제나 상황에 대해 두 가지 다른 방식으로 생각할 수 있는 상황을 말합니다. "가상의"라는 단어는 이러한 상황이 현실적이지 않거나 아직 증명되지 않았음을 의미합니다.
- "P의 두 가지 버전"은 'P'라는 개념이나 문제에 대해 두 가지 다른 관점이나 해석이 있을 수 있다는 것을 나타냅니다.
- "A가 무엇인지에 따라..."는 'A'라는 변수나 조건에 따라 상황이 변할 수 있다는 것을 의미합니다. 즉, A의 값에 따라 우리가 특정 상황에 있을 수도 있고, 그렇지 않을 수도 있다는 것입니다.
이 문장은 계산 이론과 관련된 내용을 다루고 있습니다. 여기에서 언급된 P^와 P는 문제의 집합을 나타내며, A는 특정 문제를 나타냅니다.
- P^는 오라클 머신(마법 같은 도구)을 사용하여 A 문제를 해결할 수 있는 문제의 집합입니다. 이 오라클은 A 문제를 즉시 해결할 수 있지만, 우리는 그 방법을 알 수 없습니다.
- 기존의 P 내에 있는 A는 일반적인 방법으로 다항 시간 내에 해결될 수 있는 문제를 의미합니다.
이 텍스트는 이 두 세계 사이의 차이점을 설명하려고 합니다. 첫 번째 세계는 마법 같은 도구(오라클)를 사용하여 문제를 해결하는 세계이며, 두 번째 세계는 일반적인 방법으로 문제를 해결하는 세계입니다.
오라클 언어 A가 각 문자열 x에 대해 x가 A에 속할 확률이 ½인 방식으로 인위적으로 생성되었다고 가정합니다.

이제 우리는 "거의 모든" 오라클 선택에 대해 P ≠ NP임을 보이고자 합니다. 좀 더 정확하게는 다음과 같습니다: 우리가 오라클 언어 A를 랜덤한 절차로 생성하되, 모든 문자열 x ∈ {0,1}*에 대해 (다른 모든 문자열과 독립적으로) A에 속하거나 속하지 않을 확률이 동일하다면 (즉, ∀x Pr[x ∈ A] = 1/2이라면)
Pr[P^A = NP^A] = 0, 즉, Pr[P^A ≠ NP^A] = 1.
물론 이로부터, P와 NP 클래스가 다른 오라클이 존재한다는 것이 따라진다.
이를 사용하여 P가 NP와 같지 않다는 것을 증명할 수 있을까요? => 랜덤 오라클 가설
"랜덤 오라클 가설"은 계산 이론에서 중요한 개념입니다. 이 가설은 P와 NP의 동등성에 관한 질문을 다루기 위해 '랜덤하게' 동작하는 가상의 오라클(결정적으로 동작하지 않는)을 도입합니다.
여기서 주어진 상황은 오라클 언어 A가 임의의 문자열 x에 대해 x가 A에 속할 확률이 정확히 ½인 방식으로 구성되었다는 것입니다. 이러한 가정 하에서, A는 매우 불규칙하고 예측 불가능한 특성을 갖게 됩니다.
랜덤 오라클 가설은 이러한 '랜덤 오라클'을 사용하여 P ≠ NP임을 증명하려고 합니다. 이 가설의 핵심 아이디어는, 대부분의 오라클에 대해 P ≠ NP라는 것을 증명함으로써, 일반적인 경우에도 P ≠ NP일 가능성이 매우 높다는 것을 나타내려는 것입니다.
그러나 랜덤 오라클 가설을 사용하여 P와 NP의 동등성 문제를 결정적으로 해결하는 것은 아직까지 성공하지 못했습니다. 이 가설은 단순히 이 문제에 대한 새로운 관점과 접근 방식을 제공합니다.
이 텍스트는 오라클을 사용하여 P와 NP의 동등성 문제에 대한 통찰력을 제공합니다. 주어진 정보는 오라클 언어 A를 랜덤하게 선택하는 방식을 설명하며, 그 결과 대부분의 오라클 선택에서 P와 NP가 다르다는 결론을 내립니다.
여기서 주요 아이디어는, 오라클 언어 A를 임의로 생성할 때 모든 문자열이 A에 속할 확률이 정확히 1/2라는 것입니다. 이러한 랜덤 선택 기준 하에서, P^A와 NP^A가 동일하다는 확률은 0이며, 따라서 P^A와 NP^A가 다르다는 확률은 1입니다.
이러한 결과로부터, 일부 특정 오라클 선택에서 P와 NP가 서로 다른 클래스임을 알 수 있습니다. 이는 P와 NP의 동등성 문제에 대한 중요한 통찰력을 제공하는 결과입니다.
랜덤 오라클 가설 – 결과적으로는 거짓이지만...

이 결과는 특히 매력적으로 보입니다: 0에서 1까지의 척도에서 바늘은 오른쪽 끝까지 가리키고 있습니다. 이것이 상대화되지 않은 문제에 대한 답, 즉, P ≠ NP에 대한 징후가 될 수 있을까요? 바로 어떤 명제가 임의의 오라클에 대해 확률 1로 성립한다면, 상대화되지 않은 명제도 성립한다고 결론지을 (또는 더 나은 추측을 할) 수 있다는 이러한 사고 방식을 랜덤 오라클 가설이라고 합니다.
이 텍스트는 컴퓨터 과학에서 중요한 주제인 P와 NP의 동등성 문제와 관련이 있습니다. 첫 번째 부분은 P ≠ NP 문제에 대한 특정 결과의 가능한 중요성과 매력성을 강조합니다. 이를 통해 "랜덤 오라클 가설"이라는 개념을 소개합니다. 이 가설은 어떤 명제가 임의의 오라클에 대해 확률 1로 성립하면, 해당 명제가 상대화되지 않은 문맥에서도 성립한다는 것을 제안합니다.
그러나 두 번째 문장은 이 가설이 결국은 거짓임을 나타냅니다. 그럼에도 불구하고, 이 가설은 P와 NP 문제와 관련된 연구에서 여전히 중요한 토론 주제입니다.

다른 NP-완전 문제의 NP-완전성입니다. 그래프 \(G = (V, E)\)의 꼭짓점 커버(vertex cover)는 \(V'\)의 부분 집합이며, 각 엣지 \((u, v) \in E\)에 대해 인접한 꼭짓점 \(u\) 및 \(v\) 중 적어도 하나를 포함합니다. 꼭짓점 커버 \(V'\)의 크기는 그것이 포함하는 고유한 꼭짓점의 수입니다. 이 개념들은 그림 6.1에 설명되어 있습니다.
꼭짓점 커버
인스턴스: 그래프 \(G = (V, E)\)와 양의 정수 \(k \leq |V|\)
질문: \(G\)에 대해 크기가 \(k\) 이하인 꼭짓점 커버가 있습니까?
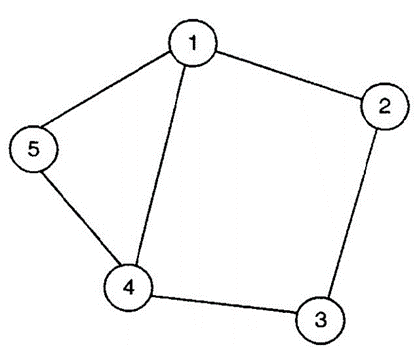
{1,3,5} – a vertex cover
{1,2,4} – a vertex cover
{2,5} – not a vertex cover
NP-완전성은 컴퓨터 과학의 복잡도 이론에서 주요한 개념입니다. NP-완전 문제는 모든 NP 문제를 다항 시간 내에 해당 문제로 변환할 수 있음을 의미합니다.
꼭짓점 커버는 그래프의 부분 집합을 나타내며, 그 부분 집합에 포함된 꼭짓점들이 그래프의 모든 엣지를 커버한다는 것을 의미합니다. 즉, 각 엣지에 대해 그 엣지의 두 꼭짓점 중 적어도 하나가 꼭짓점 커버에 포함되어 있어야 합니다.
제시된 그림에서는 5개의 꼭짓점을 가진 그래프를 보여주고 있습니다. 꼭짓점 커버의 예로는 꼭짓점 1, 3, 5가 있을 수 있습니다. 이 꼭짓점들은 그래프의 모든 엣지를 커버하기 때문입니다.