Passive vs Active Reinforcement Learning
"Passive vs Active Reinforcement Learning"은 강화 학습 내에서 두 가지 다른 접근 방식을 설명합니다:
- Passive Reinforcement Learning (수동 강화 학습):
- 고정된 정책: 수동 강화 학습에서 에이전트는 주어진, 변경되지 않는 정책을 따릅니다. 이 정책은 에이전트가 어떤 상태에서 어떤 행동을 취할지 정해주지만, 에이전트는 이 정책을 변경할 수 없습니다.
- 환경 탐색 없음: 에이전트는 환경을 탐색하거나 새로운 전략을 시도하지 않습니다. 대신, 이미 정해진 정책에 따라 행동합니다.
- 목표: 주어진 정책의 효과를 평가하고, 이를 통해 상태의 가치를 학습하는 것입니다. 여기서 에이전트는 최적의 행동을 결정하기보다는 주어진 정책 내에서 최선을 다하는 방법을 배웁니다.
- Active Reinforcement Learning (능동 강화 학습):
- 정책 탐색: 능동 강화 학습에서 에이전트는 다양한 행동을 시도하고 결과를 관찰함으로써 최적의 정책을 스스로 발견합니다. 이는 에이전트가 환경과의 상호작용을 통해 학습하고, 정책을 지속적으로 개선하는 과정을 포함합니다.
- 환경 탐색: 에이전트는 새로운 행동을 시도하고 다양한 상태를 경험하면서 환경을 탐색합니다. 이는 에이전트가 더 나은 결정을 내릴 수 있도록 합니다.
- 목표: 최적의 정책을 찾아내어 장기적으로 가장 높은 보상을 얻는 것입니다. 여기서 에이전트는 환경에 대한 지식을 확장하고, 이를 바탕으로 최적의 행동을 결정합니다.
수동 강화 학습은 이미 정해진 정책 내에서 학습하는 반면, 능동 강화 학습은 환경과의 지속적인 상호작용을 통해 최적의 정책을 탐색하는 데 초점을 맞춥니다.
Model-Based RL
"Model-Based RL"은 강화 학습(Reinforcement Learning, RL)의 한 방식으로, 이는 환경의 모델을 명시적으로 학습하고 이를 사용하여 최적의 정책을 결정하는 접근 방법입니다. 모델 기반 강화 학습의 주요 특징과 절차는 다음과 같습니다:
- 환경 모델의 학습: 모델 기반 RL의 첫 단계는 환경의 모델을 학습하는 것입니다. 이 모델은 에이전트가 취할 수 있는 행동과 이 행동들이 환경에 미치는 영향을 예측합니다. 주로, 상태 전이 확률(어떤 상태에서 특정 행동을 했을 때 다른 상태로 이동할 확률)과 보상 함수(각 행동에 대한 보상)를 포함합니다.
- 모델을 이용한 정책 결정: 학습된 모델을 바탕으로 최적의 정책을 찾습니다. 이 과정에서 계획 알고리즘(예: 동적 계획법, 몬테카를로 트리 검색)을 사용하여 다양한 행동 시나리오를 시뮬레이션하고, 가장 좋은 결과를 가져올 행동을 결정할 수 있습니다.
- 이점:
- 효율성: 모델을 사용하면 실제 환경에서의 시행 착오 없이도 행동의 결과를 예측할 수 있어 학습 과정이 더 효율적일 수 있습니다.
- 계획 및 예측: 에이전트는 모델을 사용하여 미래의 상태와 보상을 예측하고, 이를 기반으로 계획을 세울 수 있습니다.
- 단점:
- 모델 정확도: 모델의 정확도가 학습 결과의 품질에 크게 영향을 미칩니다. 부정확한 모델은 잘못된 정책을 초래할 수 있습니다.
- 복잡한 환경: 매우 복잡하거나 예측하기 어려운 환경에서는 정확한 모델을 구축하기 어려울 수 있습니다.
모델 기반 RL은 환경에 대한 이해를 바탕으로 보다 계획적이고 효율적인 학습을 추구하는 반면, 모델이 환경을 얼마나 잘 반영하는지가 성공의 열쇠가 됩니다.
- 모델 기반 아이디어:
- 경험을 바탕으로 근사 모델 학습
- 학습된 모델이 정확하다고 가정하고 가치를 해결
- 단계 1: 경험적 MDP 모델 학습
- 각 s, a에 대한 결과 s’ 계산
- 계산된 수치를 바탕으로 T(s,a,s’)의 각 항목 직접 추정
- 전이를 경험할 때 각 R(s,a,s’) 발견
- 단계 2: 학습된 MDP 해결
- 예를 들어, 이전과 같이 가치 또는 정책 반복 사용
- 모델 기반 아이디어 (Model-Based Idea):
- 경험을 바탕으로 한 근사 모델 학습: 이 접근법은 에이전트가 경험을 통해 환경의 모델을 근사적으로 학습하는 것을 기반으로 합니다. 이는 실제 환경에서의 상태 전이와 보상을 관찰하고 이를 모델화하는 과정을 포함합니다.
- 학습된 모델을 정확하다고 가정하여 가치 해결: 에이전트는 학습된 모델이 정확하다고 가정하고, 이를 바탕으로 최적의 정책을 찾습니다.
- 단계 1: 경험적 MDP 모델 학습 (Learn empirical MDP model):
- 결과 계산: 각 상태(s)와 행동(a) 쌍에 대해 이어지는 결과 상태(s’)를 계산합니다.
- 전이 확률 추정: 계산된 결과를 사용하여 전이 확률 T(s,a,s’)를 직접 추정합니다.
- 보상 발견: 전이를 경험할 때마다, 해당 전이에 대한 보상 R(s,a,s’)을 발견합니다.
- 단계 2: 학습된 MDP 해결 (Solve the learned MDP):
- 가치 또는 정책 반복 사용: 학습된 모델을 바탕으로, 가치 반복(value iteration)이나 정책 반복(policy iteration)과 같은 알고리즘을 사용하여 최적의 정책을 찾습니다.
이 방법은 에이전트가 실제 환경에서의 상태 전이와 보상을 관찰하고, 이를 바탕으로 모델을 구축하여 최적의 정책을 결정하는 과정을 포함합니다.
Example: Model-Based Learning

모델 기반 학습(Model-Based Learning) 과정의 한 예를 나타내고 있습니다. 이 과정은 크게 세 부분으로 나뉩니다:
- 입력 정책 π (Input Policy π): 이 그리드는 상태 공간을 나타냅니다. 여기서 각각의 셀(예: A, B, C, D, E)은 가능한 상태를 나타내며, 화살표는 주어진 정책 π에 따른 각 상태에서의 권장 행동을 나타냅니다. 감마(γ)는 할인 계수(discount factor)를 나타내며, 이는 미래 보상을 현재 가치로 할인하는 데 사용됩니다. 여기서 γ=1은 미래의 보상을 현재 가치와 같게 취급한다는 것을 의미합니다.
- 관찰된 에피소드 (Observed Episodes (Training)): 이 부분은 학습 과정 중에 에이전트가 관찰한 에피소드를 나타냅니다. 실제 환경에서 에이전트는 입력 정책에 따라 행동하고, 이 결과로부터 얻은 데이터(상태 전이와 받은 보상)를 수집합니다. 이러한 데이터는 모델을 학습하는 데 사용됩니다.
- 학습된 모델 (Learned Model): 이 섹션은 학습 과정을 통해 구축된 모델을 나타냅니다. 이 모델에는 두 가지 주요 구성 요소가 있습니다:
- T(s,a,s’): 상태 전이 확률을 나타냅니다. 즉, 상태 s에서 행동 a를 취했을 때 다른 상태 s’로 이동할 확률입니다.
- R(s,a,s’): 보상 함수를 나타냅니다. 이는 상태 s에서 행동 a를 취해 상태 s’로 이동했을 때 에이전트가 받게 되는 보상의 값을 나타냅니다.
이미지에서는 실제로 학습된 내용의 세부 사항이 보이지 않지만, 이 과정에서 에이전트는 관찰된 에피소드를 통해 상태 전이 확률과 보상 함수를 학습하고, 이를 사용하여 최적의 정책을 결정하거나 예측을 수행할 수 있습니다. 이 모델을 사용하여 에이전트는 실제 환경에서 시행 착오 없이, 혹은 제한된 시행 착오로 효율적으로 최적의 정책을 찾을 수 있습니다.
Pros and Cons
- 장점:
- 경험을 효율적으로 활용한다 (낮은 샘플 복잡성).
- 단점:
- 큰 상태 공간에 대해 확장이 어려울 수 있다.
- 한 번에 하나의 상태-행동 쌍에 대한 모델을 학습한다 (하지만 이는 해결 가능한 문제다).
- 매우 큰 |𝑆|에 대한 MDP를 해결할 수 없다 (이 또한 어느 정도 해결 가능하다).
- 환경이 부분적으로 관찰 가능할 때 훨씬 더 어렵다.
- 큰 상태 공간에 대해 확장이 어려울 수 있다.
장점 (Pros):
- 경험의 효율적 활용: 모델 기반 강화 학습은 수집된 데이터(즉, 에이전트의 경험)를 최대한 활용하여 모델을 구축합니다. 적은 수의 샘플을 사용하여도 효과적으로 학습할 수 있기 때문에, 샘플 복잡성이 낮습니다.
단점 (Cons):
- 큰 상태 공간에 대한 확장성 문제: 모델 기반 접근법은 큰 상태 공간을 가진 문제에서는 확장성에 문제가 있을 수 있습니다. 모든 상태-행동 쌍에 대한 모델을 학습해야 하므로, 상태 공간의 크기가 증가함에 따라 계산 부담이 커집니다. 그러나 이는 함수 근사 방법이나 다른 기법을 사용하여 어느 정도 해결할 수 있습니다.
- 매우 큰 |𝑆|에 대한 MDP 해결의 어려움: 매우 큰 상태 공간을 가진 마르코프 결정 과정(MDP)을 해결하는 것은 계산적으로 매우 어려울 수 있습니다. 이 문제 역시 상태 공간의 압축이나 근사 방법을 통해 해결할 수 있습니다.
- 부분 관찰 가능 환경의 어려움: 환경의 모든 요소가 완전히 관찰 가능하지 않을 때(예: 에이전트가 관찰할 수 없는 숨겨진 상태가 있을 때) 모델을 정확하게 학습하고 예측하는 것은 훨씬 더 복잡합니다. 이는 추가적인 기법이나 알고리즘을 필요로 합니다.
이러한 장단점은 모델 기반 강화 학습을 적용할 때 고려해야 할 중요한 요소입니다.
Model-Free Learning
모델-프리 학습(Model-Free Learning)은 강화 학습(RL)의 한 형태로, 에이전트가 환경의 모델을 명시적으로 학습하지 않고도 최적의 정책을 찾습니다. 이 접근 방식에서 에이전트는 환경의 동작 방식을 이해하거나 예측하기보다는 경험을 통해 직접 최적의 행동을 학습합니다. 모델-프리 학습의 주요 특징은 다음과 같습니다:
- 직접적인 가치 함수 또는 정책 추정:
- 모델-프리 접근법은 상태 또는 상태-행동 쌍의 가치를 직접 추정합니다. 이는 가치 기반 방법론(예: Q-러닝) 또는 정책 기반 방법론(예: 정책 그래디언트)을 통해 이루어질 수 있습니다.
- 환경과의 상호작용을 통한 학습:
- 에이전트는 환경과 상호작용하면서 얻은 보상을 기반으로 학습합니다. 에이전트는 시행착오를 통해 어떤 행동이 좋은 결과를 가져오는지 배웁니다.
- 시행착오를 통한 탐색과 활용의 균형:
- 에이전트는 탐색(exploration)을 통해 새로운 행동을 시도하고, 활용(exploitation)을 통해 알려진 좋은 행동을 사용합니다. 이 균형은 최적의 학습 성과를 달성하기 위해 중요합니다.
- 환경의 모델에 대한 무지:
- 모델-프리 학습은 상태 전이 확률이나 보상 함수를 명시적으로 추정하거나 학습하지 않습니다. 즉, 에이전트는 환경이 어떻게 반응할지에 대한 내부 모델을 구축하지 않습니다.
모델-프리 학습의 장점은 계산 복잡성이 낮고, 구현이 비교적 간단하며, 복잡한 환경에서도 잘 작동할 수 있다는 것입니다. 그러나 단점은 보통 더 많은 시행착오와 데이터를 필요로 하며, 때로는 학습 과정이 느릴 수 있다는 점입니다.
Basic Idea of Model-Free Methods
모델-프리 방법의 기본 아이디어:
- 분포에 대한 기대값을 근사하기 위해서는 다음 두 가지 방법 중 하나를 사용할 수 있습니다:
- 샘플에서 분포를 추정하고 기대값을 계산합니다.
- 분포를 우회하고 샘플에서 직접 기대값을 추정합니다.
모델-프리 방법의 기본 개념은 주어진 정책 또는 행동에 대한 보상의 기대값을 직접적으로 추정하는 것입니다. 이 방법은 환경의 모델(즉, 상태 전이 확률과 보상 함수)을 알 필요가 없습니다. 대신, 에이전트는 환경과의 상호작용을 통해 얻은 샘플(경험)을 사용하여 다음 두 가지 방법 중 하나로 기대값을 근사합니다:
- 분포 추정 후 기대값 계산:
- 이 방법은 먼저 샘플을 사용하여 확률 분포를 추정한 다음, 이 분포를 사용하여 기대값을 계산합니다. 이는 통계적 추정 방법을 사용하여 분포를 모델링하는 과정을 포함합니다.
- 직접 기대값 추정:
- 이 접근법은 분포를 명시적으로 모델링하지 않고, 대신 샘플에서 직접 기대값을 추정합니다. 이 방법은 통계적으로 평균을 내거나, 강화 학습에서 사용되는 기법(예: Q-러닝)을 사용하여, 보상의 합계 또는 평균을 계산함으로써 기대값을 추정합니다.
모델-프리 방법은 특히 환경 모델이 복잡하거나 알려지지 않았을 때 유용하며, 에이전트가 직접 경험을 통해 학습할 수 있도록 합니다.
Example: Expected Age

이 이미지는 모델 기반(Model-Based)과 모델-프리(Model-Free) 방법을 사용하여 기대값을 추정하는 방법을 비교 설명하고 있습니다.

이 예에서는 '기대 나이'를 계산하는 것으로 보입니다. 모델 기반 방법은 연령의 분포를 추정하고 이를 사용하여 기대 연령을 계산하는 반면, 모델-프리 방법은 관찰된 연령 샘플들을 직접 사용하여 기대 연령을 추정합니다. 각 방법은 다른 가정과 계산 절차를 사용하지만, 충분한 데이터가 주어지면 비슷한 결과를 도출할 수 있습니다.
Passive Reinforcement Learning
- 단순화된 과제: 정책 평가
- 입력: 고정된 정책 π(𝑠)
- 전이 확률 𝑇과 보상 𝑅을 모릅니다.
- 목표: 상태 가치 𝑉^𝜋(𝑠) 학습
수동 강화 학습 (Passive Reinforcement Learning):

수동 강화 학습의 핵심은 에이전트가 활동적으로 환경을 변경하거나 최적의 정책을 찾는 것이 아니라, 주어진 정책이 환경에서 얼마나 잘 작동하는지를 평가하고 이해하는 것입니다. 이를 통해 에이전트는 정책이 특정 환경에서 얼마나 좋은 성과를 내는지를 평가할 수 있습니다.
Direct Evaluation
- 직접 평가
- 목표: 𝑉^𝜋(𝑠)를 추정합니다, 즉, 상태 𝑠부터의 예상 총 할인된 보상
- 아이디어:
- 반환값을 사용합니다, 상태 𝑠부터 실제로 누적된 할인 보상의 합
- 여러 번의 시도와 상태 𝑠 방문에 대해 평균을 냅니다
- 이를 직접 평가(또는 직접 유틸리티 추정)라고 합니다
직접 평가 (Direct Evaluation):
- 목표 (Goal): 에이전트는 주어진 정책 � 하에서 상태 �에서 시작하여 미래에 얻을 수 있는 할인된 보상의 기대 총액, 즉 상태 가치 ��(�)를 추정하려고 합니다.
- 아이디어 (Idea):
- 실제로 관찰된 반환값, 즉 각 시도에서 상태 �부터 받은 보상을 할인한 후 더한 값을 사용합니다.
- 상태 �를 여러 번 방문하고 여러 시도를 거쳐서 얻은 반환값들의 평균을 내어 상태 가치를 추정합니다.
- 직접 평가 방법 (Direct Evaluation Method):
- 이 방법은 각 상태의 가치를 직접적으로 계산하는 방식입니다. 이는 복잡한 모델을 만들지 않고, 간단히 관찰된 데이터만을 사용하여 각 상태의 유틸리티 또는 가치를 추정합니다.
- 이 접근법은 계산이 간단하며, 특히 상태 방문 횟수가 많을수록 더 정확한 추정이 가능합니다.
직접 평가는 모델이 없는 상태에서도 각 상태의 유용성을 평가할 수 있게 해주는 간단하지만 효과적인 방법입니다.
Example: Direct Estimation

이 이미지는 강화 학습의 수동 접근법 중 하나인 직접 평가(Direct Estimation)의 예시를 보여줍니다. 직접 평가는 강화 학습 과정에서 상태의 가치를 직접적으로 계산하는 방법입니다. 각 부분에 대한 설명은 다음과 같습니다:
- 입력 정책 π (Input Policy π):
- 여기서는 각 상태(A, B, C, D, E)에 대해 정책이 어떤 행동을 권장하는지 보여줍니다. 각 상태에는 화살표로 표시된 권장 행동이 있습니다.
- 할인 계수 γ(감마)는 1로 설정되어 있으며, 이는 미래의 보상을 현재 가치로 할인하지 않겠다는 것을 의미합니다.
- 관찰된 에피소드 (Observed Episodes (Training)):
- 실제 훈련 과정에서 에이전트가 관찰한 에피소드가 여기에 기록될 것입니다. 하지만 이 이미지에는 구체적인 에피소드 내용이 나타나지 않고 있습니다.
- 출력 값 (Output Values):
- 각 상태(A, B, C, D, E)의 계산된 가치가 나타나 있습니다. 이 값들은 해당 상태에서 시작하여 정책 π를 따랐을 때 얻을 수 있는 예상 총 할인된 보상을 나타냅니다.
- 예를 들어, 상태 A는 -10의 값을 가지는데, 이는 상태 A가 낮은(부정적인) 보상을 가져오는 상태임을 의미합니다. 반면에 상태 D는 +10의 값을 가지고, 이는 상태 D가 높은(긍정적인) 보상을 가져오는 상태임을 나타냅니다.
직접 평가 방법에서는 이러한 값들을 얻기 위해 여러 번의 시도와 해당 상태의 방문을 통해 얻은 반환값들(할인된 보상의 합)의 평균을 사용합니다. 이 과정을 통해 정책의 성능을 직접적으로 평가할 수 있습니다.
Problems with Direct Estimation
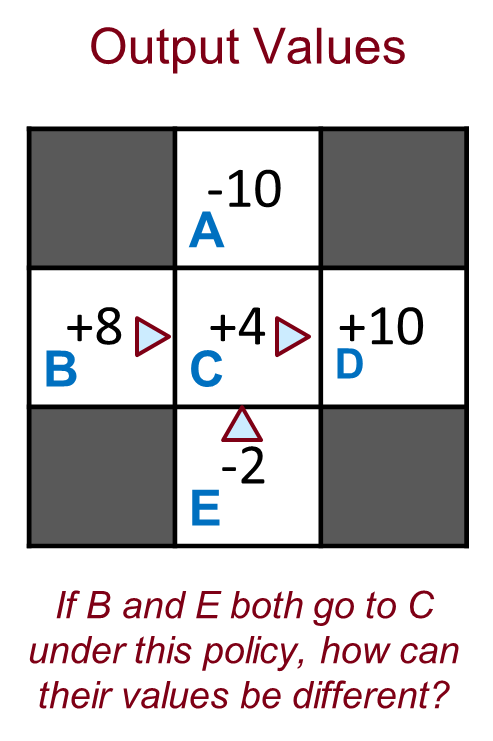
- 직접 평가의 장점은 무엇인가요?
- 이해하기 쉽습니다.
- 전이 확률 𝑇과 보상 𝑅에 대한 지식이 필요하지 않습니다.
- 한계에서 올바른 답에 수렴합니다.
- 직접 평가의 단점은 무엇인가요?
- 각 상태를 개별적으로 학습해야 합니다 (수정 가능).
- 상태 연결에 대한 정보를 무시합니다.
- 그래서 학습하는데 오랜 시간이 걸립니다.
(예를 들어, B=집에서, 열심히 공부하기 E=도서관에서, 열심히 공부하기 C=자료를 알고, 시험 보러 가기)
- 출력 값
- 이 정책 하에서 B와 E 모두 C로 간다면, 그들의 가치가 어떻게 다를 수 있나요?
직접 평가의 장점:
- 직접 평가는 각 상태에서의 반환값(받은 보상의 합)을 사용하여 상태 가치를 추정하는 간단한 방법입니다.
- 복잡한 환경 모델을 구축할 필요가 없으며, 수집된 데이터만으로 상태 가치를 학습할 수 있습니다.
- 충분한 시간과 데이터가 주어지면, 정확한 상태 가치 추정에 도달할 수 있습니다.
직접 평가의 단점:
- 각 상태는 개별적으로 학습되어야 하며, 이는 효율성을 저하시킬 수 있습니다. 그러나 이는 모델 학습 방식 등의 다른 기법을 통해 개선할 수 있습니다.
- 상태 간의 연결 또는 상태 전이에 대한 정보를 활용하지 않기 때문에, 학습 과정이 더 오래 걸릴 수 있습니다. 상태 간의 연결성을 고려하는 것은 학습 과정을 가속화할 수 있습니다.
출력 값에서의 문제:
- 이미지에 제시된 문제는 상태 B와 E가 모두 C로 향할 때, 각각의 상태 가치가 어떻게 다를 수 있는지에 대한 것입니다. 직접 평가에서는 B와 E의 상태 가치가 다르게 나타나는데, 이는 각 상태의 경험된 반환값에 기반한 평균에 따라 달라질 수 있습니다. 실제 환경에서 B와 E가 같은 행동을 취했더라도, 다른 상태를 경유하거나 다른 보상을 받았을 수 있기 때문에 가치가 다를 수 있습니다. 이는 직접 평가 방법이 각 상태를 독립적으로 평가한다는 한계를 보여줍니다.
Temporal Difference (TD) Learning
시간차(Temporal Difference, TD) 학습은 강화 학습의 한 형태로, 에이전트가 경험을 통해 직접 학습하는 모델-프리 방법입니다. TD 학습의 핵심 아이디어는 추정된 가치 함수를 실제로 받은 보상과 다음 상태의 추정 가치를 기반으로 점진적으로 수정하는 것입니다. 이 접근법은 에이전트가 환경과 상호작용하면서 학습하므로, 환경에 대한 전이 확률이나 보상 함수를 명시적으로 알 필요가 없습니다.
TD 학습의 기본적인 방법 중 하나는 TD(0)이라고도 하는데, 이는 다음과 같이 작동합니다:

TD 학습은 에이전트가 경험을 바탕으로 예측을 점진적으로 개선할 수 있게 해주며, 특히 비연속적인 환경이나 온라인 상황에서 유용합니다. TD 학습은 또한 다른 강화 학습 알고리즘, 예를 들어 Q-러닝이나 사르사(SARSA)와 같은 방법의 기초가 됩니다.
TD as Approximate Bellman Update


이러한 방법은 각 상태를 방문할 때마다 상태의 가치를 점진적으로 업데이트하고, 여러 번의 에피소드를 통해 가치 함수가 실제 가치에 수렴하도록 합니다. TD 학습은 환경에 대한 명시적인 모델이 없어도 각 상태의 가치를 추정할 수 있게 해주는 강력한 방법입니다.

이 내용은 TD 학습의 또 다른 핵심 아이디어로, 각 상태-행동 쌍 후의 전이에 따라 해당 상태의 가치를 업데이트하는 방법을 설명하고 있습니다. 이것은 벨만 방정식을 근사하는 방식으로 진행됩니다.
- 각 상태에서 에이전트가 특정 행동을 취했을 때 얻는 보상과, 그 행동으로 인해 도달한 다음 상태의 할인된 가치를 사용하여 현재 상태의 가치를 업데이트합니다.
- 이 업데이트는 시간차 학습의 한 형태로, 실제로 에이전트가 경험한 전이를 기반으로 합니다.
- 예를 들어, 상태 [3,1]에서 'up' 행동을 취한 후 상태 [3,2]로 이동했다면, [3,1]의 가치는 [3,1]에서 'up' 행동을 했을 때의 보상과 상태 [3,2]의 현재 추정 가치를 사용하여 업데이트됩니다.
- 할인 계수 는 미래의 가치를 현재 가치에 얼마나 중요하게 반영할 것인지를 결정합니다.
- 이 과정은 정책 하에 각 상태에서 최적의 행동을 취했을 때 예상되는 누적 보상을 반영하여 상태의 가치를 점진적으로 수정해 나가는 것입니다.
아이디어 3 :실행 중인 평균(running average)을 유지하면서 가치를 업데이트
실행 중인 평균(running average)을 유지하면서 가치를 업데이트하는 방법은 시간차(TD) 학습에서 각 상태의 가치 추정치를 점진적으로 조정하는 방법입니다. 이 접근법은 각 상태를 방문할 때마다 얻은 새로운 보상 정보를 기존의 가치 추정치에 통합하여 가치 추정치를 업데이트합니다.
이 방법은 다음과 같은 프로세스를 따릅니다:

이러한 방식으로 TD 학습은 벨만 방정식의 근사치를 사용하여, 효과적으로 에이전트의 경험을 바탕으로 상태 가치를 업데이트합니다. 상태 가치의 실행 중인 평균을 유지함으로써, 에이전트는 지속적인 학습을 통해 가치 함수가 진정한 가치 함수에 점점 더 가까워지도록 할 수 있습니다.
Running Averages
- 1, 4, 7의 평균을 어떻게 계산하나요?
- 방법 1: 모두 더하고 N으로 나눕니다.
- 1+4+7=12
- µ=12/N=12/3=4
- 방법 2: 실행 중인 평균 µ_n과 실행 중인 카운트 n을 유지합니다.
- n=0 µ_0=0
- n=1 µ_1=(0∙µ_0+x_1)/1 =(0∙0+1)/1=1
- n=2 µ_2=(1∙µ_1+x_2)/2 =(1∙1+4)/2=2.5
- n=3 µ_3=(2∙µ_2+x_3)/3 =(2∙2.5+7)/3=4
- 일반 공식: µ_n=((n−1)∙µ_(n−1)+x_n)/n =(n−1)/n µ_(n−1)+1/n x_n (이전 평균과 새 샘플의 가중 평균)
이 내용은 두 가지 방법으로 평균을 계산하는 방법을 설명하고 있습니다. 첫 번째 방법은 간단하게 모든 값을 더한 후 개수로 나누는 전통적인 평균 계산 방법입니다. 두 번째 방법은 실행 중인 평균을 계산하는 방법으로, 새로운 데이터 포인트가 추가될 때마다 평균을 업데이트합니다.
실행 중인 평균(running average) 방법:
- 이 방법은 새로운 샘플이 추가될 때마다 평균을 갱신하며, 각 단계에서 이전의 평균값에 새로운 값을 통합합니다.
- 이 과정은 각 새 샘플을 추가할 때마다 평균을 재계산하는 대신, 기존 평균에 새 샘플을 점진적으로 통합하는 방식입니다.
- 가중 평균(weighted average)은 이전 평균과 새 샘플 사이의 균형을 맞추기 위해 사용되며, 새 샘플이 전체 평균에 미치는 영향을 조절합니다.
이 방법은 데이터 스트림이나 실시간 데이터 처리에 유용하며, 데이터 포인트가 순차적으로 수신되는 경우에 특히 적합합니다. TD 학습에서 이 방법은 상태 가치를 업데이트할 때 이전 추정치와 새로운 보상을 효율적으로 통합하는 데 사용됩니다.

가중 평균을 사용하는 방법은 각 샘플에 고정된 가중치 를 적용하여 평균을 계산합니다. 이 방법은 가장 최근의 샘플에 더 큰 가중치를 부여하고, 이전 샘플들의 가중치는 지수적으로 감소시킵니다. 이러한 방식을 지수적 잊음(exponential forgetting)이라고 하며, 오래된 데이터에 대한 영향을 점점 줄이고 새로운 데이터의 영향을 더 반영합니다.

이 접근법은 특히 온라인 학습이나 실시간 데이터 처리에 유용하며, TD 학습과 같은 강화 학습 알고리즘에서 상태 가치를 업데이트하는 데 자주 사용됩니다.
TD as Approximate Bellman Update

이 과정은 시간차(Temporal Difference, TD) 학습의 기본적인 원리를 설명하고 있습니다. TD 학습은 현재 상태의 가치를 샘플(즉시 보상 + 할인된 다음 상태의 가치)을 통해 업데이트함으로써 진행됩니다.
- 샘플: 이는 상태 에서 정책 에 의해 선택된 행동을 취했을 때의 보상과, 그 결과 도달한 다음 상태 ′의 할인된 가치 합계입니다.
- TD 오류: 샘플과 현재 추정 가치 사이의 차이로, 학습 과정에서 이 오류를 줄이는 방향으로 가치 추정치를 조정합니다.
- 학습률 : 이는 새로운 샘플이 현재 가치 추정치에 얼마나 영향을 미칠지를 결정합니다. 학습률이 높으면 새로운 샘플에 더 빠르게 반응하지만, 너무 높으면 학습 과정이 불안정해질 수 있습니다.
결과적으로 TD 학습은 현재 상태의 가치를 새로운 샘플로 조금씩 업데이트하면서, 시간이 지남에 따라 점진적으로 이웃 상태의 가치와 일관성을 높여 갑니다. 이는 강화 학습 에이전트가 경험을 통해 학습하고, 정책의 성능을 개선할 수 있도록 돕는 중요한 메커니즘입니다.
Example: Temporal Difference Learning
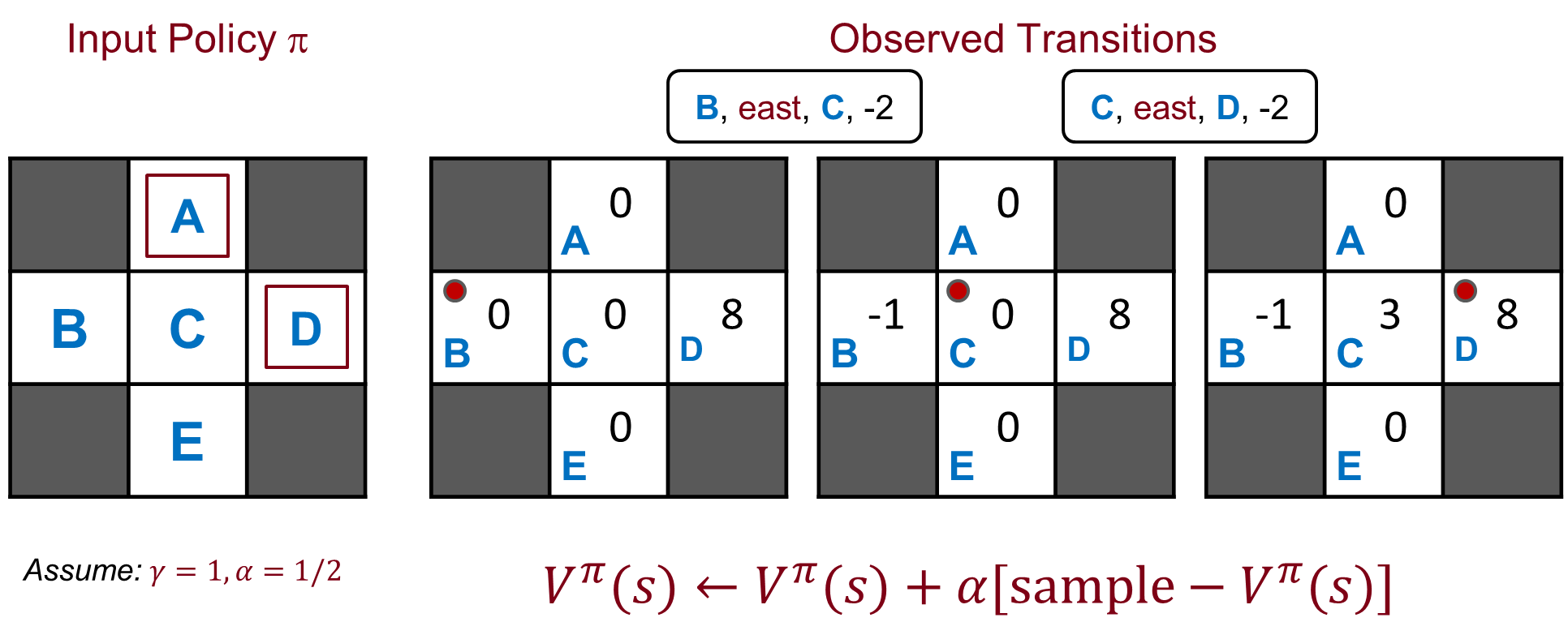
이 이미지는 시간차(Temporal Difference, TD) 학습의 예시를 시각적으로 보여주고 있습니다. TD 학습은 현재 상태의 가치를 추정하고, 경험을 통해 이 추정치를 점차적으로 수정해 가는 과정입니다.
이미지의 설명은 다음과 같습니다:

이 방식은 강화 학습 에이전트가 얻은 경험을 바탕으로 효과적으로 학습할 수 있도록 합니다. 할인 계수를 1로 설정함으로써, 미래의 가치를 현재 가치와 동일하게 취급하고 있으며, 이는 특정한 학습 문제 설정에 따른 것일 수 있습니다.
Problems with TD Value Learning ( TD 가치 학습의 문제점 )
- TD 가치 학습은 벨만 업데이트를 모방하여 실행 중인 샘플 평균으로 정책 평가를 수행하는 모델-프리 방법입니다.
- 하지만 전이 모델 없이는 가치 함수를 사용하거나 한 단계 탐욕스러운 예상 최대화(expectimax)를 통해 정책을 개선할 수 없습니다!
- (나중에 큰 상태 공간에서 알려진 모델을 사용하여 이를 활용하는 방법을 살펴볼 것입니다)
TD 가치 학습의 문제점:
- TD 가치 학습은 환경에 대한 전이 모델이 없이도 에이전트가 경험을 바탕으로 정책의 성능을 평가할 수 있게 하는 기법입니다. 이는 벨만 방정식에 기초한 업데이트를 실행 중인 샘플의 평균을 사용하여 근사합니다.
- 그러나 가치 함수만으로는 최적의 행동을 결정하거나 정책을 개선할 충분한 정보가 없습니다. 이는 정책을 개선하기 위해서는 각 상태에서 가능한 모든 행동의 결과를 예측할 수 있는 전이 모델이 필요함을 의미합니다.
- 예상 최대화(expectimax) 접근법은 각 상태에서 가능한 모든 행동의 기대 가치를 계산하여 가장 좋은 행동을 선택하는 방법입니다. 이를 위해서는 각 행동 후의 가능한 모든 결과 상태들과 그 결과들이 발생할 확률, 즉 전이 모델이 필요합니다.
추후 살펴볼 내용:
- TD 학습과 같은 모델-프리 방법은 큰 상태 공간을 가진 문제에서 유용합니다. 이러한 상황에서는 전이 모델을 완전히 알기 어렵거나 모델을 구축하는 것이 계산상 비효율적일 수 있습니다.
- 나중에는 큰 상태 공간에서 알려진 모델을 사용하여 TD 학습을 어떻게 적용할 수 있는지 살펴보게 됩니다. 이는 일반적으로 모델 기반 접근법과 TD 학습의 특정한 통합을 의미할 수 있으며, 이를 통해 에이전트는 더 효율적으로 학습하고 정책을 개선할 수 있습니다.
Q-Learning as Approximate Q-Iteration

Q-러닝은 강화 학습의 한 형태로, 에이전트가 어떤 상태에서 특정 행동을 취했을 때 예상되는 미래 보상의 총합을 학습하는 모델-프리 방법입니다.
- 값은 상태 에서 행동 를 취한 뒤에 최적으로 행동하며 얻을 수 있는 예상 리턴을 나타냅니다. 값은 상태 에서 가능한 모든 행동에 대해 최대의 값을 선택함으로써 얻을 수 있는 최적의 가치를 의미합니다.
- 벨만 방정식은 이 이상적인 값을 얻기 위한 재귀적인 관계를 정의합니다. 이 방정식은 현재 상태와 행동에서 예상되는 보상과 다음 상태에서의 최적 행동에 대한 가치의 합을 나타냅니다.
- 근사 벨만 업데이트는 실제로 환경의 전이 확률을 모르기 때문에 이상적인 값을 직접 계산할 수 없을 때 사용됩니다. 대신, 경험을 통해 얻은 샘플 과 현재 추정치 를 바탕으로 값을 업데이트합니다.
- 이러한 방식으로 값을 업데이트하면, 전이 모델이 없어도 에이전트는 경험을 통해 최적의 행동을 학습할 수 있습니다. 그러나 테이블은 상태별로 가능한 모든 행동에 대한 값을 저장해야 하므로, 테이블에 비해 상당히 큰 저장 공간이 필요합니다.
이러한 테이블은 각 상태에서 에이전트가 취할 수 있는 모든 행동에 대한 가치를 포함하며, 이를 통해 정책을 유도할 수 있습니다. 이 정책은 각 상태에서 테이블을 기반으로 가장 높은 가치를 갖는 행동을 선택하는 것입니다.
Q-Learning

위 내용은 Q-러닝 알고리즘의 핵심 메커니즘을 설명하고 있습니다. Q-러닝은 강화 학습의 모델-프리 방법으로, 에이전트가 환경으로부터 샘플을 받고, 이를 사용하여 행동-가치 함수 를 업데이트합니다.
- 샘플 받기: 에이전트는 상태 에서 행동 를 취해 새로운 상태 ′로 전이하고, 그 과정에서 보상 을 받습니다.
- 샘플 추정치: 새 샘플 추정치는 즉시 보상 과 할인된 다음 상태 ′에서 가능한 모든 행동 ′에 대한 최대 값의 합으로 계산됩니다. 이는 현재 상태-행동 쌍에 대한 기대 리턴을 나타냅니다.
- 실행 중인 평균 통합: 이전 추정치에 새 샘플 추정치를 합산하여 업데이트하는 과정입니다. 이때 학습률 는 새 샘플이 값에 미치는 영향의 정도를 결정합니다.
이러한 방식으로, Q-러닝은 각 상태-행동 쌍에 대해 에이전트가 얻은 경험을 바탕으로 값을 점진적으로 조정합니다. 결과적으로, 에이전트는 최적의 정책을 학습할 수 있으며, 이는 각 상태에서 가능한 최대 값을 갖는 행동을 선택함으로써 얻어집니다. Q-러닝은 특히 전이 확률이나 보상 함수를 명시적으로 모델링하지 않아도 적용할 수 있는 강력한 방법입니다.
Q-Learning Demo – Gridworld
그리드에서 맨 오른쪽 값의 보상이 5.0~9.96으로 늘어난다. (결국 10.0이 됨) 그에 따라 그 쪽으로 갈 수 록 얻을 수 있는 기대 가치도 늘어난다.
근데 아래에서 하나의 보상 가치가 -50.0~100.00으로 변하는데 이러면 아래쪽으로 행동했을 때 기대 가치가 음수값으로 계속 가는 모습이 보인다.
Q-Learning Demo – Crawler
크롤러에서도 그리드가 있는데 포크레인 로봇팔의 팔 끝의 움직임이 어디에 있냐에 따라 초록색~빨간색으로 기대값이 보이는거 같다.
Q-Learning Properties
- 놀라운 결과: Q-러닝은 최적의 정책으로 수렴합니다 – 샘플이 최적이 아닌 정책에서 생성되더라도 말이죠!
- 이를 오프-폴리시 학습이라고 합니다.
- 주의 사항:

Q-러닝의 속성에 대한 설명입니다. Q-러닝은 강화 학습 알고리즘 중 하나로, 에이전트가 경험을 통해 학습하면서 최적의 정책을 찾아내는 과정입니다.
- 오프-폴리시 학습: Q-러닝은 실제로 수행 중인 정책과 상관없이 최적의 정책을 학습할 수 있는 오프-폴리시 학습 방법입니다. 이는 에이전트가 현재 사용하고 있는 정책이 최적이 아니더라도, 관측된 데이터로부터 최적의 행동 방식을 배울 수 있음을 의미합니다.
- 주의사항:

Summary
- 강화 학습(RL)은 전이와 보상에 대한 직접적인 경험을 통해 마르코프 결정 과정(MDPs)을 해결합니다.
- 여러 가지 방식이 있습니다:
- MDP 모델을 학습하고 그것을 해결합니다.
- 보상의 합계에서 직접 �를 학습하거나, TD(Temporarl Difference) 지역 조정을 통해 학습합니다.
- 여전히 앞을 내다보며 결정을 내리기 위한 모델이 필요합니다.
- 지역 Q-러닝 조정을 통해 Q를 학습하고, 이를 직접 사용하여 행동을 선택합니다.
- (그리고 약 100가지 다른 변형들)
- 큰 빠진 부분들:
- 너무 큰 후회 없이 어떻게 탐색할 수 있을까요?
- 이를 테트리스(10^60), 바둑(10^172), 스타크래프트(행동의 수 ∣�∣=1026)처럼 큰 규모로 어떻게 확장할 수 있을까요?
강화 학습은 상태와 행동을 기반으로 하는 환경에서 최적의 결정을 내리는 과정을 컴퓨터 알고리즘을 통해 모델링합니다. 강화 학습의 목표는 최적의 정책을 찾아내는 것으로, 이 정책은 에이전트가 얻을 수 있는 총 보상을 최대화하는 행동 시퀀스를 결정합니다.
다양한 강화 학습 알고리즘들은 이러한 목표를 다양한 방식으로 달성하려 시도합니다. 일부는 환경의 모델을 명시적으로 학습하고 최적화 문제를 해결하려 시도합니다. 다른 방법으로는, 직접적인 보상의 합이나 시간차 학습을 통해 가치 추정치를 조정함으로써 모델을 학습하지 않고도 최적의 행동을 결정합니다.
하지만 강화 학습의 큰 도전 중 하나는 효율적인 탐색과 큰 규모의 문제를 해결하는 것입니다. 효율적인 탐색은 에이전트가 불확실한 환경에서 최대의 보상을 얻기 위해 안전하면서도 과감한 탐색을 수행하는 것을 의미합니다. 큰 규모의 문제를 해결하는 것은, 계산 가능한 시간 안에 상태 공간이 매우 크거나 행동의 수가 많은 문제에 대해 최적의 정책을 찾는 것을 의미합니다.