Outline
- 기본 법칙들 (Basic Laws)
- 주변 분포 (Marginal Distribution)
- 조건부 분포 (Conditional Distribution)
- 곱셈 및 연쇄 규칙 (Product and Chain Rules)
- 추론 (Inference)
- 독립성 (Independence)
- 조건부 독립 (Conditional Independence)
- 기본 법칙들: 확률론의 기본적인 법칙들을 의미합니다. 이에는 확률의 합계 법칙, 곱셈 법칙, 및 전체 확률의 법칙 등이 포함될 수 있습니다.
- 주변 분포: 확률 변수 집합 내에서 일부 변수에만 관심을 가질 때, 이 변수들의 확률 분포를 말합니다. 예를 들어, 두 변수 와 의 결합 분포에서 의 주변 분포를 구하는 것입니다.
- 조건부 분포: 한 확률 변수의 분포가 다른 변수의 특정 값에 의존하는 경우의 분포입니다. 예를 들어, �가 주어졌을 때 의 분포를 로 나타냅니다.
- 곱셈 및 연쇄 규칙: 여러 확률 변수의 결합 확률을 그들의 조건부 확률과 주변 확률의 곱으로 나타내는 법칙입니다. 연쇄 규칙은 변수들의 순서에 따라 결합 확률을 분해하는 방법을 제공합니다.
- 추론: 관찰된 데이터를 바탕으로 미지의 확률 변수의 분포를 추정하는 과정입니다. 이는 베이지안 추론 및 다양한 통계적 추론 방법론을 포함할 수 있습니다.
- 독립성: 두 확률 변수가 서로에게 영향을 주지 않을 때, 즉 하나의 변수의 값이 다른 변수의 분포에 영향을 주지 않을 때 이 변수들은 독립적이라고 합니다.
- 조건부 독립: 두 변수가 세 번째 변수에 대한 조건 하에 독립적인 관계를 가질 때, 이를 조건부 독립이라고 합니다. 예를 들어, 와 가 에 대해 조건부 독립일 경우, 가 주어졌을 때 와 는 서로 독립적입니다.
Uncertainty
- 불확실성 (Uncertainty)
- 실제 세계는 불확실성으로 가득 차 있습니다!
- 예를 들어, 비행기 출발 60분 전에 SFO 공항으로 출발한다면 제시간에 도착할 수 있을까요?
- 실제 세계는 불확실성으로 가득 차 있습니다!
- 문제점들 (Problems):
- 부분적 관측 가능성 (도로 상태, 다른 운전자들의 계획 등)
- 잡음이 많은 센서 (라디오 교통 보고, 구글 지도)
- 교통, 보안 검사 등의 모델링과 예측의 엄청난 복잡성
- 세계 역학에 대한 지식 부족 (타이어가 터질까요? 코로나 검사가 필요할까요?)
- 확률론적 주장들은 무지와 게으름의 영향을 요약합니다
- 확률 이론 + 효용 이론의 결합 → 의사결정 이론
- 기대 효용을 최대화:
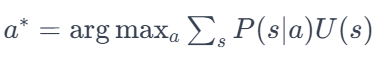
- 불확실성: 실제 세계는 예측할 수 없는 다양한 요소로 가득 차 있습니다. 예를 들어, 비행기 시간에 맞춰 공항에 도착할 수 있을지 예측하는 것은 여러 불확실한 요소에 의존합니다.
- 문제점들:
- 부분적 관측 가능성: 우리는 항상 모든 필요한 정보를 가지고 있지 않습니다. 예를 들어, 도로 상황이나 다른 운전자의 계획과 같은 변수들은 종종 불분명합니다.
- 잡음이 많은 센서: 교통 정보와 같은 데이터는 종종 정확하지 않을 수 있습니다.
- 모델링 및 예측의 복잡성: 교통 흐름이나 보안 검사 대기 시간과 같은 요소들은 예측하기 매우 복잡합니다.
- 세계 역학에 대한 지식 부족: 예기치 못한 상황(예: 타이어 펑크, 건강 검진 필요)은 예측하기 어렵습니다.
- 확률론적 주장들: 이는 우리가 가지고 있는 불완전한 정보와 한계를 요약하여 표현하는 방법입니다.
- 의사결정 이론: 확률 이론과 효용 이론을 결합하여 최적의 결정을 내리는 이론입니다. 여기서는 가능한 모든 시나리오에 대해 기대 효용을 계산하고, 그 효용을 최대화하는 행동을 선택합니다. 이 공식은 주어진 행동 에 대해 가능한 모든 상태 에 대한 확률 과 그 상태의 효용 을 고려하여 최적의 행동을 선택하는 방법을 나타냅니다.