Rejection Sampling

- 조건부 확률을 추정하기 위한 사전 샘플링의 간단한 응용
- 예를 들어, 𝑃(𝐶|𝑟, 𝑤)=𝛼𝑃(𝐶, 𝑟, 𝑤)를 추정하고자 할 때
- 이러한 카운트를 위해서는 ¬𝑟 또는 ¬𝑤를 가진 샘플은 관련이 없습니다.
- 따라서 𝑟, 𝑤를 가진 샘플에서 𝐶의 결과를 세고, 나머지 샘플을 모두 버립니다.
- 이것이 바로 rejection sampling(거부 샘플링)이라고 불리며
- 이 방법은 조건부 확률에 대해 일관된 결과를 얻을 수 있습니다.
- 즉, 극한에서 정확한 결과를 얻을 수 있습니다.
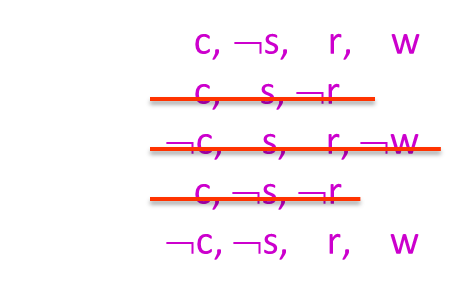
Rejection Sampling(거부 샘플링)은 조건부 확률을 추정하기 위한 간단한 샘플링 방법 중 하나입니다. 이 방법은 다음과 같이 동작합니다:
- 우리가 원하는 조건부 확률을 예를 들어 𝑃(𝐶|𝑟, 𝑤)=𝛼𝑃(𝐶, 𝑟, 𝑤)와 같이 설정합니다. 여기서 𝑃(𝐶, 𝑟, 𝑤)는 관심 조건부 확률입니다.
- 이 조건에 해당하는 샘플을 생성하기 위해 사전 샘플링을 수행합니다. 이때, ¬𝑟 또는 ¬𝑤를 가진 샘플은 관련이 없으므로 무시합니다.
- 즉, 𝑟과 𝑤를 가진 샘플에서만 𝐶의 결과를 세고, 나머지 샘플은 모두 버립니다. 이로써 관심 있는 조건에 해당하는 샘플만을 남기게 됩니다.
- 이렇게 선택된 샘플들을 사용하여 조건부 확률을 추정할 수 있습니다.
Rejection Sampling은 조건부 확률을 추정하는 데에 활용되며, 극한에서는 정확한 결과를 얻을 수 있는 일관된 방법입니다. 그러나 샘플 중에 버려지는 비율이 크면 비효율적일 수 있으므로 효율적인 샘플링을 위해서는 다른 방법들도 고려할 수 있습니다.
입력: evidence (𝑒_1,…,𝑒_𝑘)
For 𝑖=1, 2, …, 𝑛
Sample 𝑋_𝑖 from 𝑃(𝑋_𝑖 |parents(𝑋_𝑖))
If 𝑥_𝑖 not consistent with evidence
Reject: Return, and no sample is generated in this cycle
Return (𝑥_1, 𝑥_2, …, 𝑥_𝑛)
For 𝑖=1, 2, …, 𝑛
𝑋_𝑖를 𝑃(𝑋_𝑖 |parents(𝑋_𝑖))에서 샘플링합니다.
만약 𝑥_𝑖가 evidence와 일치하지 않으면
거부합니다: 결과를 반환하고 이 단계에서는 샘플이 생성되지 않습니다.
(𝑥_1, 𝑥_2, …, 𝑥_𝑛)을 반환합니다.
Rejection Sampling(거부 샘플링)은 확률 분포로부터 샘플을 추출하면서 주어진 증거(evidence)를 만족시키는 샘플만을 남기는 샘플링 방법입니다. 다음은 Rejection Sampling의 동작 방식을 설명합니다:
- 입력으로는 주어진 증거 evidence (𝑒_1,…,𝑒_𝑘)가 있습니다.
- 변수 𝑋_𝑖 (𝑖=1, 2, …, 𝑛)를 확률 분포 𝑃(𝑋_𝑖 |parents(𝑋_𝑖))에서 샘플링합니다. 이는 각 변수를 그 부모(parents) 변수들의 값에 따라 조건부 확률 분포에서 샘플링하는 것을 의미합니다.
- 𝑥_𝑖가 evidence와 일치하지 않는 경우, 이 샘플을 거부합니다. 이것은 evidence와 일치하지 않는 샘플이 무시되고 해당 사이클에서는 샘플이 생성되지 않음을 의미합니다.
- 모든 변수에 대한 샘플링이 완료되면, 남은 샘플들을 반환합니다. 이때, 반환되는 샘플들은 주어진 evidence를 만족하는 것들로 구성됩니다.
Rejection Sampling은 조건부 확률을 추정하거나 베이지안 네트워크에서 추론을 수행할 때 유용한 방법 중 하나이며, 주어진 증거를 고려하여 확률 분포로부터 효과적으로 샘플을 생성할 수 있습니다.
Car Insurance: 𝑃(PropertyCost|𝑒)


설명은 나중에 추가
Likelihood Weighting ( 가능도 가중치)
- 거부 샘플링의 문제점:
- 증거(evidence)가 매우 낮은 확률로 발생할 경우, 많은 샘플을 거부합니다.
- 샘플을 추출하는 동안 증거가 활용되지 않습니다.
- 예를 들어, 𝑃(Shape|Color=blue)와 같은 조건부 확률을 고려해보세요.

- 아이디어: 증거 변수를 고정하고 나머지 변수를 샘플링합니다.
- 문제: 샘플 분포가 일관되지 않음!
- 해결책: 각 샘플을 가중치로 조절하여 증거 변수가 주어진 경우 부모 변수에 대한 확률을 고려합니다.

가능도 가중치(Likelihood Weighting)는 거부 샘플링(Rejection Sampling)의 단점을 극복하기 위한 확률 추론 방법 중 하나입니다.
거부 샘플링의 문제점은 증거(evidence)가 발생할 확률이 매우 낮을 경우, 많은 샘플을 거부하여 효율적이지 않다는 것입니다. 또한, 샘플을 추출하는 동안 증거가 활용되지 않아 낭비가 발생합니다.
가능도 가중치는 이러한 문제를 해결하기 위해 아이디어를 제공합니다. 이 방법은 다음과 같이 작동합니다:
- 먼저, 증거 변수를 고정하고 evidence에 해당하는 값을 설정합니다.
- 나머지 변수들을 확률 분포에 따라 샘플링합니다. 이 과정에서는 evidence가 고정된 상태로 변수들을 무작위로 추출합니다.
- 샘플링한 결과를 사용하여 조건부 확률을 계산합니다. 이때, 샘플들은 증거에 맞게 가중치를 부여합니다. 즉, 증거 변수가 주어진 경우, 각 샘플의 가중치는 증거 변수의 값에 대한 조건부 확률 분포를 반영합니다.
이러한 방식으로 가능도 가중치는 evidence가 주어진 상황에서 베이지안 네트워크의 조건부 확률을 추정하는 데 사용됩니다. 이 방법은 rejection sampling의 단점을 극복하면서 증거를 활용하여 효율적으로 확률을 계산할 수 있게 해줍니다.

설명은 나중에 추가
입력: evidence 𝑒1,..,𝑒𝑘 , 𝑤 = 1.0
for 𝑖=1, 2, …, 𝑛
if 𝑋_𝑖 is an evidence variable
𝑥_𝑖 = observed value for 𝑋_𝑖
Set 𝑤=𝑤×𝑃(𝑥_𝑖 |parents(𝑋_𝑖))
else
Sample 𝑥_𝑖 from 𝑃(𝑋_𝑖 |parents(𝑋_𝑖))
return (𝑥_1, 𝑥_2, …, 𝑥_𝑛), 𝑤
𝑖=1부터 𝑛까지 반복
- 만약 𝑋_𝑖가 증거 변수인 경우
- 𝑥_𝑖 = 𝑋_𝑖의 관측값(observed value)으로 설정
- 𝑤 = 𝑤 × 𝑃(𝑥_𝑖 |parents(𝑋_𝑖))로 설정
- 그렇지 않으면
- 𝑃(𝑋_𝑖 |parents(𝑋_𝑖))에서 𝑥_𝑖를 샘플링
- 𝑤는 그대로 유지 반환 (𝑥_1, 𝑥_2, …, 𝑥_𝑛), 𝑤
가능도 가중치(Likelihood Weighting)는 베이지안 네트워크에서 조건부 확률을 추정하는 확률적인 방법입니다. 이 방법은 증거(evidence)가 주어진 상황에서 주변 변수들을 샘플링하여 조건부 확률을 추정하는 방식으로 동작합니다.
다음은 가능도 가중치의 동작 방식입니다:
- 먼저, 입력으로 주어진 증거 변수들에 해당하는 값을 설정합니다. 이러한 변수들은 이미 주어진 증거로 고정됩니다.
- 나머지 변수들에 대해서는 다음과 같이 처리합니다:
- 변수 𝑋_𝑖가 증거 변수가 아닌 경우, 이 변수를 해당하는 조건부 확률 분포 𝑃(𝑋_𝑖 |parents(𝑋_𝑖))에서 샘플링합니다.
- 변수를 샘플링할 때, 각 변수의 부모(parents) 변수들의 값을 활용하여 샘플을 추출합니다.
- 이 과정을 반복하여 모든 변수에 대한 값을 추출합니다. 이때, 주어진 증거에 해당하는 변수는 이미 설정된 값이며, 나머지 변수는 샘플링을 통해 얻은 값이 됩니다.
- 마지막으로, 확률 값 𝑤를 초기화한 후에 각 변수의 샘플에 대한 조건부 확률을 곱하여 가중치를 계산합니다. 이 가중치는 주어진 증거에 대한 조건부 확률 분포를 반영합니다.
- 샘플링된 변수들과 가중치를 반환합니다. 이를 통해 조건부 확률을 추정할 수 있습니다.
가능도 가중치는 증거가 주어진 상황에서 조건부 확률을 추정하는 데 사용되며, 샘플링을 통해 확률 값을 계산하므로 확률적인 결과를 얻을 수 있습니다.
Likelihood Weighting is Consistent ( 우도 가중치는 일관적임)
- Z가 샘플링되고 e가 고정된 증거인 경우의 샘플링 분포 𝑆_WS (𝑧,𝑒)=∏2_𝑗▒〖𝑃(𝑧_𝑗 |parents(𝑍_𝑗))〗
- 이제, 샘플들은 가중치를 가짐 𝑤(𝑧,𝑒)=∏2_𝑘▒〖𝑃(𝑒_𝑘 |parents(𝐸_𝑘))〗
- 함께하면, 가중된 샘플링 분포는 일관됨 𝑆_WS (𝑧,𝑒)⋅𝑤(𝑧,𝑒)=∏2_𝑗▒〖𝑃(𝑧_𝑗 |parents(𝑍_𝑗))〗 ∏2_𝑘▒〖𝑃(𝑒_𝑘 |parents(𝐸_𝑘))〗 =𝑃(𝑧,𝑒)
- 우도 가중치는 중요도 샘플링의 예시임
- 𝑃로부터의 샘플을 기반으로 어떤 양을 추정하고자 함
- 𝑃에서 샘플링하기 어렵기 때문에 대신 𝑄를 사용함
- 각 샘플 𝑥에 대해 𝑃(𝑥)/𝑄(𝑥)로 가중치를 부여함
우도 가중치(Likelihood Weighting)에 대해 설명하겠습니다. 이 방법은 확률적 모델에서 특정 조건하의 확률을 추정하는 데 사용됩니다. 이 방법은 중요도 샘플링(Importance Sampling)의 한 예로, 특정 확률 분포에서 직접 샘플링하기 어려울 때 사용됩니다.
- 샘플링 분포 𝑆_WS (𝑧,𝑒): 이 식은 Z가 샘플링되고 e가 고정된 증거(evidence)일 때의 분포를 나타냅니다. 여기서 각 Z의 자식 노드(𝑍_𝑗)에 대한 확률 𝑃(𝑧_𝑗 | parents(𝑍_𝑗))의 곱으로 표현됩니다.
- 샘플의 가중치 𝑤(𝑧,𝑒): 샘플링된 각 Z에 대해, 고정된 증거 e에 대한 가중치를 계산합니다. 이 가중치는 고정된 증거의 각 요소(𝑒_𝑘)에 대한 조건부 확률 𝑃(𝑒_𝑘 | parents(𝐸_𝑘))의 곱으로 계산됩니다.
- 가중된 샘플링 분포의 일관성: 샘플링 분포와 샘플의 가중치를 곱하면, 최종적으로 Z와 e에 대한 결합 확률 분포 𝑃(𝑧,𝑒)를 얻을 수 있습니다. 이는 샘플링 분포와 가중치가 함께 작동하여 원하는 확률 분포를 일관되게 추정한다는 것을 의미합니다.
- 중요도 샘플링의 적용: 우도 가중치는 중요도 샘플링의 한 형태입니다. 이는 원하는 분포 𝑃에서 직접 샘플링하는 것이 어려울 때, 다른 분포 𝑄에서 샘플링하고 각 샘플을 𝑃(𝑥)/𝑄(𝑥)로 가중치를 주어 원래 분포의 특성을 추정하는 방법입니다.
간단히 말해서, 우도 가중치는 확률적 모델에서 특정 조건 하에서 원하는 확률을 효율적으로 추정하기 위해 샘플링 분포와 가중치를 결합하는 방법입니다. 이 방법은 복잡한 확률 모델에서 특정 조건하의 확률을 계산하는 데 매우 유용합니다.
Car Insurance: 𝑃(PropertyCost|𝑒)

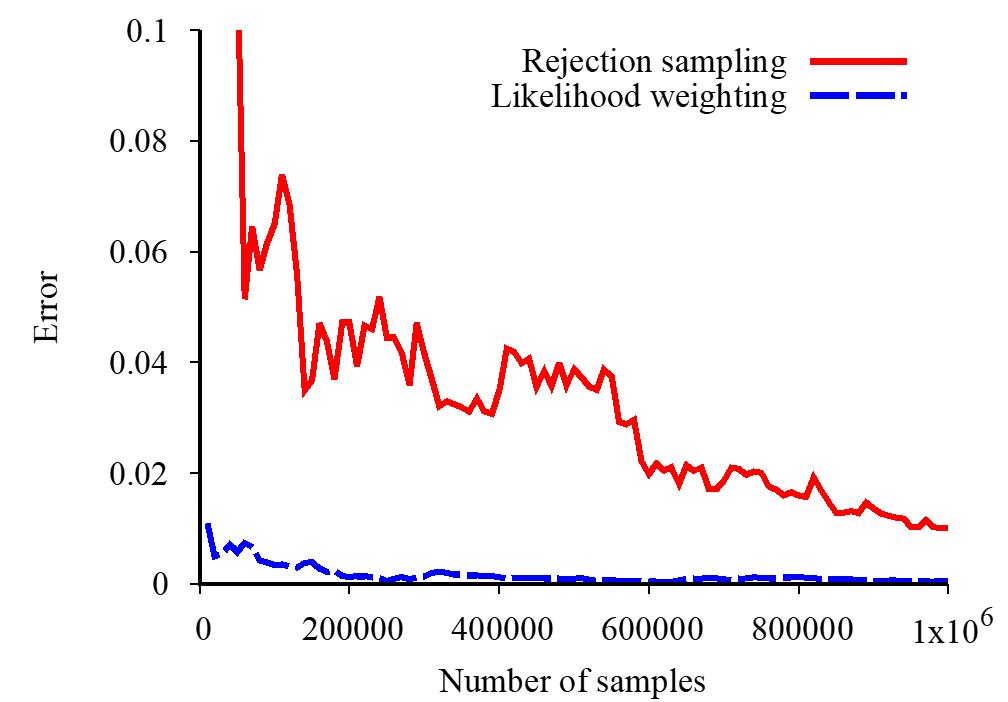
설명은 나중에 추가
Likelihood Weighting
- 가능성 가중치는 좋습니다.
- 우리는 샘플을 생성하면서 증거를 고려했습니다.
- 예를 들어, 여기에서 𝑊의 값은 𝑆, 𝑅의 증거 값에 따라 선택됩니다.
- 더 많은 샘플이 증거에 의해 제안된 세계의 상태를 반영할 것입니다.
- 가능성 가중치는 모든 문제를 해결하지는 않습니다.
- 증거는 하류 변수의 선택에 영향을 미치지만 상류 변수에는 영향을 미치지 않습니다 (𝐶는 증거와 일치하는 값을 더 확률적으로 얻지 않습니다).
- 우리는 모든 변수를 샘플링할 때마다 증거를 고려하고 싶습니다 (이것은 Gibbs 샘플링으로 이어집니다).
이 글은 "가능성 가중치(Likelihood Weighting)"라는 확률 추론 방법에 대한 설명을 제공하고 있습니다. 아래 내용을 설명해드리겠습니다:
- 가능성 가중치는 좋습니다:
- 가능성 가중치 방법은 확률 그래프에서 특정 변수들의 확률 분포를 추론하는 데 사용되는 방법 중 하나입니다.
- 이 방법을 사용하면 확률 분포를 추정할 때 증거(또는 관측된 정보)를 고려할 수 있습니다.
- 예를 들어, 어떤 변수 𝑊의 값을 추정할 때, 증거로 주어진 변수인 𝑆와 𝑅의 값에 따라 가능성 가중치 방법을 사용하여 𝑊의 값을 추론할 수 있습니다.
- 이로써 우리는 더 많은 샘플이 증거에 의해 제안된 세계의 상태를 반영하게 됩니다.
- 가능성 가중치는 모든 문제를 해결하지는 않습니다:
- 가능성 가중치 방법은 증거가 하류 변수(즉, 증거와 직접적으로 연결된 변수)의 선택에 영향을 미치지만 상류 변수(증거와 간접적으로 연결된 변수)에는 영향을 미치지 않습니다.
- 예를 들어, 상류 변수인 𝐶는 증거와 일치하는 값을 얻을 확률이 높아지지 않습니다.
- 우리는 모든 변수를 샘플링할 때마다 증거를 고려하고 싶습니다:
- 가능성 가중치 방법은 일부 변수에만 증거를 고려하고, 상류 변수에는 적용되지 않는 한계가 있습니다.
- 이런 경우, 모든 변수에 대해 증거를 고려하여 확률 분포를 추정하는 것이 더 바람직합니다. 이것이 Gibbs 샘플링과 같은 방법으로 이어집니다.
즉, 이 글은 가능성 가중치 방법의 장점과 한계에 대한 설명을 제공하고 있으며, 더 나은 확률 추론을 위해 더 복잡한 샘플링 방법이 필요할 수 있음을 언급하고 있습니다.

설명은 나중에 추가
Gibbs Sampling
- 절차: 모든 변수 𝑥_1, 𝑥_2, …, 𝑥_𝑛의 전체 인스턴스를 추적합니다.
- 증거와 일치하는 임의의 인스턴스로 시작합니다.
- 한 번에 하나의 변수를 샘플링하되, 나머지 모든 변수에 대한 조건부로, 증거는 고정된 채로 유지합니다.
- 이를 오랜 시간 동안 반복합니다.
- 특성: 이것을 무한히 반복하는 한, 결과 샘플들은 올바른 분포에서 나온 것으로 수렴합니다 (즉, 증거에 조건을 걸은 분포에서 샘플링됩니다).
- 합리적인 이유: 상류와 하류 변수 모두 증거에 조건을 거는 것을 고려합니다.
기브스 샘플링(Gibbs Sampling)은 확률 그래프 모델에서 변수들의 결합 확률 분포를 추정하는데 사용되는 몬테 카를로(Monte Carlo) 샘플링 방법 중 하나입니다. 아래 내용을 설명해 드리겠습니다:
- 절차:
- 기브스 샘플링은 모든 변수들의 전체 인스턴스(값들)를 추적합니다.
- 시작할 때, 증거(즉, 주어진 정보)와 일치하는 임의의 변수 인스턴스로 초기화합니다.
- 그런 다음, 한 번에 한 변수를 샘플링하고, 나머지 모든 변수들에 대해 조건부 확률로 샘플링합니다. 이때, 증거는 고정된 상태로 유지됩니다.
- 이 단계를 오랜 시간 동안 반복합니다.
- 특성:
- 기브스 샘플링은 무한히 반복할 경우, 결과 샘플들이 올바른 결합 확률 분포에서 추출된 것으로 수렴합니다. 이것은 결국 증거에 조건을 걸어서 원하는 분포를 얻는 데 사용됩니다.
- 합리적인 이유:
- 기브스 샘플링의 핵심 아이디어는 모든 변수가 서로 조건부로 연결되어 있다는 것입니다. 따라서 하나의 변수를 변경하고 나머지 변수들은 그 변경된 변수에 대한 조건부로 업데이트됩니다. 이렇게 하면 증거를 고려한 확률 분포를 고려할 수 있으며, 모든 변수에 대한 샘플을 추출할 수 있습니다.
기브스 샘플링은 베이지안 네트워크와 같이 확률적 그래프 모델을 효과적으로 활용하고, 증거를 고려하여 변수의 결합 확률 분포를 추정하는 데 유용한 기법 중 하나입니다.
Gibbs Sampling Example: 𝑃(𝑆|𝑟)
- 단계 1: 증거 고정
- 𝑅 = 𝑡𝑟𝑢𝑒 (증거값을 고정합니다).

- 단계 2: 다른 변수 초기화
- 임의로 초기화합니다.

- 단계 3: 반복
- 증거가 아닌 변수 𝑋를 선택합니다.
- 𝑋를 𝑃(𝑋|𝑋의 마르코프 블랭킷(Markov Blanket))에서 새로 샘플링합니다.

이 예제는 기브스 샘플링을 사용하여 조건부 확률 𝑃(𝑆|𝑟)를 추정하는 과정을 단계별로 설명하고 있습니다. 아래는 각 단계에 대한 설명입니다:
- 단계 1: 증거 고정
- 이 단계에서는 확률적 추론을 시작하기 전에 증거 변수를 고정합니다.
- 예를 들어, 𝑅 변수의 값이 'true'라고 가정합니다. 이것은 이미 알려진 정보 또는 주어진 증거입니다.
- 단계 2: 다른 변수 초기화
- 나머지 변수들을 무작위로 초기화합니다. 이 단계에서는 𝑆 변수를 제외한 다른 모든 변수에 임의의 초기 값을 할당합니다.
- 단계 3: 반복
- 이제 기브스 샘플링 반복을 시작합니다.
- 매 반복에서는 다음 두 단계를 수행합니다:
- a. 증거가 아닌 변수 𝑋를 선택합니다. 이 변수를 샘플링하려는 변수로 선택합니다.
- b. 선택된 변수 𝑋를 해당 변수의 마르코프 블랭킷(Markov Blanket)에 대한 조건부 확률 분포인 𝑃(𝑋|markov_blanket(𝑋))에서 새로운 값을 샘플링합니다.
이렇게 선택된 변수들의 값들을 반복적으로 업데이트하면, 기브스 샘플링은 조건부 확률 𝑃(𝑆|𝑟)를 추정하는 데 사용됩니다. 이러한 반복적인 샘플링을 통해 우리는 𝑆 변수의 값에 대한 조건부 확률 분포를 얻을 수 있습니다.
- 조건부 확률의 정의
- 합산을 도입하고 항을 제거합니다.
- 베이즈 네트워크의 정의
- 합산 항을 밖으로 이동합니다.
- 항을 제거합니다.
Efficient Resampling of One Variable
- 𝑃(𝑆|𝑐, 𝑟, ¬𝑤)에서 샘플링
- 𝑃(𝑆│𝑐,𝑟,¬𝑤)=𝑃(𝑆,𝑐,𝑟,¬𝑤)/𝑃(𝑐,𝑟,¬𝑤) = 𝑃(𝑆,𝑐,𝑟,¬𝑤)/(∑2_𝑠▒𝑃(𝑠,𝑐,𝑟,¬𝑤) ) =(𝑃(𝑐)𝑃(𝑆|𝑐)𝑃(𝑟|𝑐)𝑃(¬𝑤|𝑆,𝑟))/(∑2_𝑠▒〖𝑃(𝑐)𝑃(𝑠|𝑐)𝑃(𝑟|𝑐)𝑃(¬𝑤|𝑠,𝑟)〗) =(𝑃(𝑐)𝑃(𝑆|𝑐)𝑃(𝑟|𝑐)𝑃(¬𝑤|𝑆,𝑟))/(𝑃(𝑐)𝑃(𝑟|𝑐)∑2_𝑠▒〖𝑃(𝑠|𝑐) 𝑃(¬𝑤|𝑠,𝑟)〗) =(𝑃(𝑆|𝑐) 𝑃(¬𝑤|𝑆,𝑟))/(∑2_𝑠▒〖𝑃(𝑠|𝑐) 𝑃(¬𝑤|𝑠,𝑟)〗)
- 많은 것들이 상쇄되고, 𝑆 변수만 남습니다!
- 더 일반적으로: 재샘플링된 변수를 가진 CPTs만 고려해야 하며, 이러한 CPTs를 함께 결합해야 합니다.
이 문장은 특정 확률 분포에서 하나의 변수를 효율적으로 재샘플링하는 방법을 설명하고 있습니다. 아래에서 각 단계를 설명하겠습니다:
- 처음으로, 우리는 확률 분포 𝑃(𝑆|𝑐, 𝑟, ¬𝑤)에서 변수 𝑆를 샘플링하려고 합니다. 여기서 𝑐, 𝑟, ¬𝑤는 다른 변수들을 나타내며, 증거가 아닌 경우입니다.
- 그런 다음, 조건부 확률을 계산합니다. 즉, 𝑃(𝑆|𝑐,𝑟,¬𝑤)은 다음과 같이 정의됩니다:
- 𝑃(𝑆│𝑐,𝑟,¬𝑤) = (𝑃(𝑆,𝑐,𝑟,¬𝑤))/(𝑃(𝑐,𝑟,¬𝑤))
- 이제 위 식을 간소화하기 위해 분자와 분모를 계산합니다. 분자에는 변수 𝑆와 관련된 요소들이 있고, 분모에는 모든 변수에 대한 조건부 확률 분포의 합이 있습니다.
- 다음 단계에서, 상쇄되는 요소들이 많아지며, 최종적으로는 변수 𝑆와 관련된 조건부 확률 𝑃(𝑆|𝑐)와 관련된 요소만 남게 됩니다.
- 이것은 변수 𝑆를 재샘플링하기 위해 필요한 조건부 확률을 나타내며, 다른 변수들의 조건부 확률을 모두 고려하지 않고도 변수 𝑆를 효율적으로 업데이트할 수 있음을 의미합니다. 이런 방식으로 많은 계산이 절약되며, 변수 𝑆에 대한 조건부 확률을 추정하는 데 사용할 수 있습니다.
일반적으로, 이 방법은 변수가 서로 어떻게 관련되어 있는지에 따라 적용 가능하며, 변수 간의 상호작용을 고려하여 효율적인 재샘플링을 수행합니다.
Car Insurance: 𝑃(PropertyCost|𝑒)

설명은 나중에 추가


설명은 나중에 추가
Further Reading on Gibbs Sampling*
- 기브스 샘플링은 샘플을 무한히 많이 재샘플링하는 한계에서 쿼리 분포 𝑃(𝑄|𝑒)에서 샘플을 생성합니다.
- 기브스 샘플링은 일반적인 메트로폴리스-헤이스팅스(Metropolis-Hastings)와 같은 더 일반적인 메트로폴리스 체인 몬테 카를로(Markov Chain Monte Carlo, MCMC) 방법의 특수한 경우입니다.
- 메트로폴리스-헤이스팅스는 더 유명한 MCMC 방법 중 하나입니다. 사실, 기브스 샘플링은 메트로폴리스-헤이스팅스의 특수한 경우 중 하나입니다.
- 몬테 카를로 방법에 대해 더 읽어볼 수 있습니다. 이것들은 단순히 샘플링 방법입니다.
"Further Reading on Gibbs Sampling"이라는 부분은 Gibbs 샘플링에 대한 추가적인 정보를 제공하고 있습니다. 아래에서 각 항목에 대한 설명을 제공하겠습니다:
- 기브스 샘플링은 쿼리 분포 𝑃(𝑄|𝑒)에서 무한히 자주 재샘플링하는 한계에서 샘플을 생성합니다.
- 이것은 Gibbs 샘플링이 어떤 확률적 추론 문제에서 샘플을 생성하는데 사용되며, 재샘플링을 계속 수행함으로써 원하는 확률 분포를 근사합니다.
- 기브스 샘플링은 일반적인 마르코프 체인 몬테 카를로(Markov Chain Monte Carlo, MCMC) 방법 중 하나로서, MCMC 방법의 특별한 경우입니다.
- MCMC는 확률 분포를 추정하거나 표본을 생성하는 방법 중 하나로, 여기에서는 메트로폴리스-헤이스팅스(Metropolis-Hastings) 방법과 관련된 언급이 있습니다.
- 메트로폴리스-헤이스팅스는 MCMC 중에서도 유명한 방법 중 하나로, Gibbs 샘플링은 이 방법의 특수한 경우 중 하나입니다.
- "Monte Carlo methods"에 대한 언급은 몬테 카를로 방법에 대한 참고 정보를 제공하고 있습니다.
- 몬테 카를로 방법은 확률 분포를 추정하거나 복잡한 계산 문제를 풀기 위해 무작위 샘플링을 사용하는 방법을 일반적으로 가리킵니다.
- "they're just sampling"라는 문장은 이러한 방법들이 본질적으로 무작위 샘플링을 수행하는 것으로 간단하게 설명하고 있습니다.
이러한 정보는 Gibbs 샘플링과 관련된 개념을 더 깊이 이해하고 싶은 사람들에게 유용할 수 있으며, 확률적 추론과 샘플링 기술에 대한 관심을 더욱 확장시킬 수 있습니다.
Bayes Net Sampling Summary
- 사전 샘플링(Prior Sampling) 𝑃:
- 𝑃(𝑥_1,…,𝑥_𝑛)에서 완전한 샘플을 생성합니다.
- 우도 가중치 샘플링(Likelihood Weighting) 𝑃(𝑄|𝒆) :
- 샘플을 가중치로 조절하여 그들이 𝒆(주어진 증거)를 얼마나 잘 예측하는지 측정합니다.
- 거부 샘플링(Rejection Sampling) 𝑃(𝑄|𝒆) :
- 𝒆와 일치하지 않는 샘플을 거부합니다.
- 기브스 샘플링(Gibbs Sampling) 𝑃(𝑄|𝒆):
- 𝒆 공간에서 방황하며 보이는 것들을 평균내어 추정합니다.
이 문장은 베이지안 네트워크(Bayes Net)에서 사용되는 다양한 확률적 샘플링 방법에 대한 요약을 제공하고 있습니다. 각 방법에 대한 간략한 설명은 다음과 같습니다:
- 사전 샘플링 (Prior Sampling) 𝑃:
- 확률적 모델에서 변수들의 결합 확률 분포 𝑃(𝑥_1,…,𝑥_𝑛)로부터 완전한 샘플을 생성하는 방법입니다. 이 방법은 각 변수를 해당 확률 분포에 따라 무작위로 샘플링하여 전체 샘플을 얻습니다.
- 우도 가중치 샘플링 (Likelihood Weighting) 𝑃(𝑄|𝒆) :
- 증거(𝒆)를 고려한 조건부 확률 분포를 추정하는 방법 중 하나입니다. 샘플을 생성하고, 각 샘플에 가중치를 할당하여 증거를 얼마나 잘 예측하는지 평가합니다.
- 거부 샘플링 (Rejection Sampling) 𝑃(𝑄|𝒆) :
- 주어진 증거(𝒆)에 대한 조건부 확률 분포를 추정하는 또 다른 방법입니다. 무작위로 샘플을 생성하고, 증거와 일치하지 않는 샘플을 거부합니다. 이 방법은 일치하지 않는 샘플을 생성하지만 계산 비용이 높을 수 있습니다.
- 기브스 샘플링 (Gibbs Sampling) 𝑃(𝑄|𝒆):
- 베이지안 네트워크 내에서 확률 변수 간의 의존성을 활용하여 조건부 확률 분포를 추정하는 방법입니다. 변수를 하나씩 선택하고 조건부 확률 분포에 따라 샘플을 생성합니다. 여러 번 반복하여 평균을 계산하여 조건부 확률을 추정합니다.
이러한 샘플링 방법은 베이지안 네트워크와 같은 확률적 모델에서 확률 분포를 추정하거나 쿼리를 해결하는 데 사용됩니다. 각 방법은 다른 장단점을 가지며, 특정 문제에 더 적합한 방법을 선택할 수 있습니다.
Summary
- 베이지안 네트워크는 조건부 독립성을 활용하여 공동 분포를 효율적으로 인코딩합니다.
- 전체 공동 확률 = 지역 조건부의 곱
- 정확한 추론 = 네트워크에서 조건부 확률의 곱의 합
- 근사 추론
- 사전 샘플링
- 거부 샘플링
- 우도 가중치 샘플링
- 기브스 샘플링
이 요약은 베이지안 네트워크에 관련된 핵심 개념을 다루고 있습니다. 각 항목에 대한 간략한 설명은 다음과 같습니다:
- 베이지안 네트워크는 조건부 독립성을 활용하여 공동 분포를 효율적으로 표현합니다.
- 베이지안 네트워크는 변수들 간의 조건부 독립성을 그래프 구조로 나타내며, 이를 통해 전체 공동 확률 분포를 지역적인 조건부 확률 분포의 곱으로 표현합니다.
- 정확한 추론은 네트워크에서 조건부 확률의 곱의 합을 계산하여 이루어집니다.
- 베이지안 네트워크를 사용하여 정확한 추론을 수행하려면, 네트워크에서 각 조건부 확률 분포의 곱의 합을 계산합니다.
- 근사적 추론은 정확한 추론 대신 근사적인 방법을 사용하여 확률 분포를 추정합니다.
- 근사 추론 방법으로는 사전 샘플링, 거부 샘플링, 우도 가중치 샘플링, 기브스 샘플링 등이 있습니다.
- 이러한 방법은 정확한 추론을 수행하기 어려운 경우에 사용되며, 확률적 모델에서 확률 분포를 근사적으로 계산하는 데 도움을 줍니다.
요약적으로, 베이지안 네트워크는 조건부 독립성을 활용하여 확률 분포를 효율적으로 표현하고, 정확한 추론과 근사적 추론을 위한 다양한 방법을 제공합니다. 이러한 기술은 확률적 모델링과 추론에 중요한 역할을 합니다.