본문 바로가기
카테고리 없음

[계산이론] Simplification of Context-Free Grammars and Normal Forms - 3

7_JUN_7 2023. 12. 16. 21:26

Review: Chomsky normal forms

  • 강의 6-1에서 (CFG 간소화)
    • 𝜆-생성 규칙은 𝑆가 null이 아닌 경우에만 제거할 수 있습니다.
    • 여기서 목표는 문법에서 모든 𝜆-생성 규칙을 제거하는 것입니다.
    • 𝑆에 𝜆-생성 규칙이 포함되어 있는 경우, 문법에서 𝜆-생성 규칙을 제거하는 것은 불가능합니다.
      • 왜냐하면 𝑆 → 𝜆는 문법(생성 규칙)에 포함되어야 하기 때문입니다.
      • 이를 제거하면 생성된 문법이 원래의 문법과 동등하지 않습니다.
  • 강의 6-2에서 (CNF 단계 (1))
    • 𝑆가 nullable 인 경우에도 𝜆-생성 규칙을 제거해야 합니다.
    • 여기서 목표는 CNF를 생성하는 것입니다.
    • 𝑆가 nullable 한 경우?
      • 먼저 이를 무시하고 모든 𝜆-생성 규칙을 제거합니다.
      • 이는 CNF 변환 단계의 마지막 단계에서 고려됩니다.
      • 따라서 최종 CNF에서의 𝑆는 여전히 nullable합니다.
  • 요약하면, 만약 𝑺가 nullable 한 경우,
    1. CFG 단순화 과정에서 모든 𝜆-생성 규칙을 제거할 수 없습니다.
    2. 여전히 CFG를 CNF로 변환할 수 있으며, 먼저 모든 𝜆-생성 규칙을 제거하고 변환 단계의 매우 끝에 𝑺 → 𝜆를 추가합니다.

A membership algorithm for CFG

  • 주어진 CFG가 생성하는 언어에 문자열이 속하는지를 결정하는 문제
    • 예시
      • 문자열 𝑤 = 𝑎𝑎𝑏𝑏𝑏가 문법이 생성하는 언어에 속하는지 결정
        • 𝑆 → 𝐴𝐵
        • 𝐴 → 𝐵𝐵 | 𝑎
        • 𝐵 → 𝐴𝐵 | 𝑏
  • CYK 알고리즘
    • J. Cocke, D.H. Younger 및 T. Kasami에 의한 구문 분석 알고리즘
    • CYK 알고리즘을 사용하여 멤버십 문제를 해결할 수 있습니다.
    • 이는 CFG가 CNF 형태일 때만 사용할 수 있습니다.
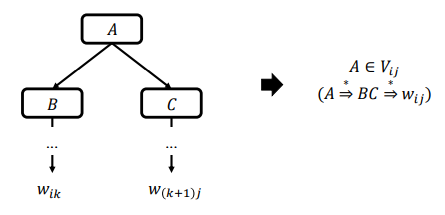
  • CYK 알고리즘: 핵심 아이디어
    • 𝐺 = 𝑉, 𝑇, 𝑆, 𝑃가 CNF 형식인 경우
    • 입력 문자열을 𝑤 = 𝑎1𝑎2 … 𝑎𝑛으로 가정합니다.
      • 우리는 부분 문자열을 정의합니다: 𝑤𝑖𝑗 = 𝑎𝑖 … 𝑎𝑗
      • 𝑉의 부분집합: 𝑉𝑖𝑗 = { 𝐴 ∈ 𝑉: 𝐴 ֜ ∗ 𝑤𝑖𝑗}
      • 𝑉𝑖𝑗 = ∪ { 𝐴: 𝐴 → 𝐵𝐶, 𝑤𝑖𝑡ℎ 𝐵 ∈ 𝑉𝑖𝑘, 𝐶 ∈ 𝑉(𝑘+1)𝑗 }
      • 그런 다음, 𝑤 ∈ 𝐿 𝐺 if and only if 𝑆 ∈ 𝑉1 𝑛

CYK 알고리즘 (Cocke-Younger-Kasami 알고리즘)은 컴퓨터 과학에서 특히 컴파일러 설계와 자연어 처리에서 널리 사용되는 알고리즘입니다. 이 알고리즘은 주어진 문자열이 특정 문법에 속하는지 여부를 결정하는 데 사용됩니다. 주로 Chomsky Normal Form (CNF)으로 변환된 문맥 자유 문법 (CFG)에 적용됩니다.

알고리즘의 핵심 아이디어는 다음과 같습니다:

  1. 문법의 CNF 변환: CYK 알고리즘은 문법이 Chomsky Normal Form에 있는 경우에만 작동합니다. CNF에서 모든 생성 규칙은 𝐴 → 𝐵𝐶 또는 𝐴 → 𝑎의 형태를 취합니다, 여기서 𝐴, 𝐵, 𝐶는 비터미널이고 𝑎는 터미널입니다.
  2. 입력 문자열: 입력 문자열 𝑤 = 𝑎1𝑎2 … 𝑎𝑛은 터미널 기호의 시퀀스입니다.
  3. 부분 문자열의 정의: 부분 문자열 𝑤𝑖𝑗는 문자열 𝑤의 𝑖번째에서 𝑗번째 기호까지의 연속적인 시퀀스입니다.
  4. 테이블의 생성: CYK 알고리즘은 𝑛×𝑛 크기의 테이블을 사용하여 각 부분 문자열을 파싱합니다. 여기서 𝑛은 입력 문자열의 길이입니다.
  5. 테이블 채우기: 테이블의 각 셀 𝑉𝑖𝑗는 비터미널의 집합입니다. 이 집합은 부분 문자열 𝑤𝑖𝑗를 생성할 수 있는 모든 비터미널을 포함합니다. 이는 𝑉𝑖𝑗 = { 𝐴 ∈ 𝑉 | 𝐴 ֜ ∗ 𝑤𝑖𝑗 }로 정의됩니다.
  6. 테이블 채우기 규칙: 𝑉𝑖𝑗는 모든 가능한 𝐵 ∈ 𝑉𝑖𝑘 및 𝐶 ∈ 𝑉(𝑘+1)𝑗에 대해, 𝐴 → 𝐵𝐶 규칙에 의해 생성될 수 있는 모든 𝐴를 포함합니다. 이는 𝑉𝑖𝑗 = ∪ { 𝐴 | 𝐴 → 𝐵𝐶, with 𝐵 ∈ 𝑉𝑖𝑘, 𝐶 ∈ 𝑉(𝑘+1)𝑗 }로 표현됩니다.
  7. 결과 판정: 문자열 𝑤가 주어진 문법 𝐺의 언어에 속하는지 여부는 테이블의 최상단 오른쪽 셀 (𝑉1𝑛)에 시작 기호 𝑆가 있는지 여부로 결정됩니다. 즉, 𝑤 ∈ 𝐿(𝐺) if and only if 𝑆 ∈ 𝑉1𝑛입니다.

CYK 알고리즘은 이러한 단계를 통해 효율적으로 주어진 문자열이 특정 문맥 자유 문법에 의해 생성될 수 있는지 판단합니다. 이는 동적 프로그래밍 기법을 사용하는 대표적인 예입니다.

 
  • • CYK 알고리즘: 핵심 아이디어
    • 문자열 𝑤𝑖𝑗를 유도할 수 있는 변수는 다음 생성 규칙을 가집니다.
      • 문자열 𝑤𝑖𝑘를 유도할 수 있는 변수와 문자열 𝑤 𝑘+1 에 유도할 수 있는 변수를 연결(concatenation)한 것
 
 

 

  • CYK 알고리즘 예제
    • 문법이 생성하는 언어에 문자열 𝑤 = 𝑎𝑎𝑏𝑏𝑏가 속하는지 결정
      • 𝑆 → 𝐴𝐵, 𝐴 → 𝐵𝐵 | 𝑎, 𝐵 → 𝐴𝐵 | 𝑏
    •  𝑉11 = {𝐴}, 𝑉22 = {𝐴}, 𝑉33 = {𝐵}, 𝑉44 = {𝐵}, 𝑉55 = {𝐵}
    • 𝑉12 = {𝐴: 𝐴 → 𝐵𝐶, 𝐵 ∈ 𝑉11, 𝐶 ∈ 𝑉22}
      • 𝐴𝐴에 대한 생성 규칙이 없음 ( 𝑉12 = ∅ )
    •  𝑉23 = {𝐴: 𝐴 → 𝐵𝐶, 𝐵 ∈ 𝑉22, 𝐶 ∈ 𝑉33}
      • 𝑆 → 𝐴𝐵 및 𝐵 → 𝐴𝐵 존재
      • 𝑉23 = {𝑆, 𝐵}
  1. 테이블 초기화: 문자열 𝑤 = 𝑎𝑎𝑏𝑏𝑏의 길이는 5이므로, 5x5 크기의 테이블을 생성합니다. 각 셀 𝑉𝑖𝑗는 𝑤의 부분 문자열 𝑤𝑖𝑗를 생성할 수 있는 비터미널의 집합을 나타냅니다.
  2. 기본 케이스 채우기: 각 𝑉𝑖𝑖 (i=1부터 5까지)에 대해, 해당 문자를 생성할 수 있는 비터미널을 채웁니다.
    • 𝑉11 = {𝐴}, 𝑉22 = {𝐴}, 𝑉33 = {𝐵}, 𝑉44 = {𝐵}, 𝑉55 = {𝐵}
  3. 테이블 채우기 (2문자 이상의 부분 문자열): 이제 두 문자 이상의 부분 문자열을 생성할 수 있는 비터미널을 찾습니다.
    • 𝑉12 = {𝐴: 𝐴 → 𝐵𝐶, 𝐵 ∈ 𝑉11, 𝐶 ∈ 𝑉22}: 여기서 𝐴𝐴는 생성 규칙에 없으므로 𝑉12 = ∅
    • 𝑉23 = {𝐴: 𝐴 → 𝐵𝐶, 𝐵 ∈ 𝑉22, 𝐶 ∈ 𝑉33}: 여기서 𝑆 → 𝐴𝐵 및 𝐵 → 𝐴𝐵 규칙이 적용될 수 있으므로 𝑉23 = {𝑆, 𝐵}
  4. 더 큰 부분 문자열에 대한 고려: 이 예제에서는 𝑉23까지만 제시되었습니다. 그러나, 전체 문자열 𝑤 = 𝑎𝑎𝑏𝑏𝑏를 고려하기 위해, 𝑉15와 같은 셀도 채워야 합니다. 이는 테이블의 나머지 부분을 계산하여 완성합니다.
  5. 결과 판단: 마지막으로, 테이블의 𝑉15 셀을 확인하여 시작 기호 𝑆가 포함되어 있는지 검사합니다. 𝑆가 𝑉15에 있다면, 문자열 𝑤는 문법에 의해 생성될 수 있음을 의미합니다.

이 예시에서는 테이블의 모든 셀을 채우지 않았기 때문에 문자열 𝑤가 문법에 의해 생성될 수 있는지의 여부를 최종적으로 결정할 수 없습니다. 완전한 판단을 위해서는 테이블의 나머지 부분을 계산해야 합니다. CYK 알고리즘은 동적 프로그래밍을 사용하여 이러한 계산을 효율적으로 수행합니다.

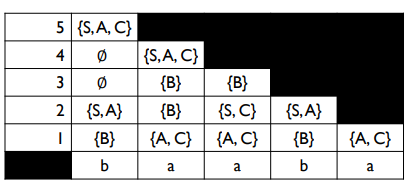
  • CYK 알고리즘 예제
    • 문법이 생성하는 언어에 문자열 𝑤 = 𝑎𝑎𝑏𝑏𝑏가 속하는지 결정
      • 𝑆 → 𝐴𝐵, 𝐴 → 𝐵𝐵 | 𝑎, 𝐵 → 𝐴𝐵 | 𝑏
    • 𝑉11 = {𝐴}, 𝑉22 = {𝐴}, 𝑉33 = {𝐵}, 𝑉44 = {𝐵}, 𝑉55 = {𝐵}
    • 𝑉12 = ∅, 𝑉23 = 𝑆, 𝐵 , 𝑉34 = 𝐴 , 𝑉45 = 𝐴
    • 𝑉13 = {𝑆, 𝐵}, 𝑉24 = 𝐴 , 𝑉35 = 𝑆, 𝐵
    • 𝑉14 = {𝐴}, 𝑉25 = 𝑆, 𝐵
    • 𝑉15 = {𝑆, 𝐵}
    • 𝑆 ∈ 𝑉15 이므로, 𝑤 ∈ 𝐿(𝐺)
 
  • CYK 알고리즘 예제
    • 문법이 생성하는 언어에 문자열 𝑤 = 𝑏𝑎𝑎𝑏𝑎가 속하는지 결정
      • 𝑆 → 𝐴𝐵 | 𝐵𝐶
      • 𝐴 → 𝐵𝐴 | 𝑎
      • 𝐵 → 𝐶𝐶 | 𝑏
      • 𝐶 → 𝐴𝐵 | 𝑎

  • CYK 알고리즘 연습
    • 문법이 생성하는 언어에 문자열 𝑤 = 𝑎𝑏𝑎𝑎𝑏가 속하는지 결정
      • 𝑆 → 𝐴𝐵 | 𝐵𝐶
      • 𝐴 → 𝐵𝐴 | 𝑎
      • 𝐵 → 𝐶𝐶 | 𝑏
      • 𝐶 → 𝐴𝐵 | 𝑎

티스토리툴바