Limitation of finite automata
- 유한 오토마타는 문맥자유 언어를 인식할 수 없습니다.
- 왜냐하면 유한 오토마타는 제한된 메모리와 저장 공간을 가지고 있기 때문입니다.
- 예를 들어, 𝐿 = {𝑎^𝑛𝑏^𝑛 | 𝑛 ≥ 1}일 때
- 유한 오토마타는 입력 문자열에 포함된 기호의 수를 세는 것이 불가능합니다.
Pushdown Automata
- 푸시다운 오토마타 (PDA)
- PDA는 본질적으로 유한 오토마타입니다.
- PDA에는 스택이라고 불리는 추가 구성 요소가 있습니다.
- 스택은 정의상 무한한 길이를 가집니다.
- 이것은 유한 오토마타에서 제한된 메모리로 인해 발생하는 한계를 극복합니다.

- (Nondeterministic) Pushdown Automata: Formal definition
- 푸시다운 오토마타 (PDA)는 7-튜플입니다: 𝑴 = (𝑸, 𝚺, 𝜞, 𝜹, 𝒒𝟎, 𝒛, 𝑭)
- 𝑸는 내부 상태의 유한한 집합입니다.
- Σ는 기호의 유한한 집합입니다.
- Γ는 스택 알파벳이라고 불리는 기호의 유한한 집합입니다.
- 𝛿는 전이 함수의 집합입니다.
- 𝛿: 𝑄 × (Σ ∪ {𝜆}) × Γ → 2^(𝑄×Γ ∗ )
- 𝑞0 ∈ 𝑸는 초기 상태입니다.
- 𝑧 ∈ Γ는 초기 스택 알파벳입니다.
- 𝐹 ⊆ 𝑸는 최종 상태의 집합입니다.
- 푸시다운 오토마타 (PDA)는 7-튜플입니다: 𝑴 = (𝑸, 𝚺, 𝜞, 𝜹, 𝒒𝟎, 𝒛, 𝑭)
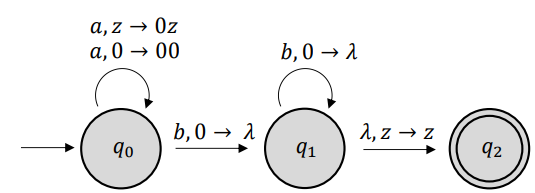
- 예시
- 𝑀 = ( {𝑞0, 𝑞1, 𝑞2} , {𝑎, 𝑏} , {0, 𝑧} , 𝛿, 𝑞0, 𝑧,{𝑞2})
- 𝛿 (𝑞0, 𝑎, 𝑧) = { (𝑞0, 0𝑧) }
- 𝛿 (𝑞0, 𝑎, 0) = { (𝑞0, 00) }
- 𝛿 (𝑞0, 𝑏, 0) = { (𝑞1, 𝜆) }
- 𝛿 (𝑞1, 𝑏, 0) = { (𝑞1, 𝜆 )}
- 𝛿 (𝑞1, 𝜆, 𝑧) = { (𝑞2, 𝑧) }
- 𝑀 = ( {𝑞0, 𝑞1, 𝑞2} , {𝑎, 𝑏} , {0, 𝑧} , 𝛿, 𝑞0, 𝑧,{𝑞2})


- 예시
- 예를 들어, 입력 문자열이 "𝑎𝑎𝑏𝑏"


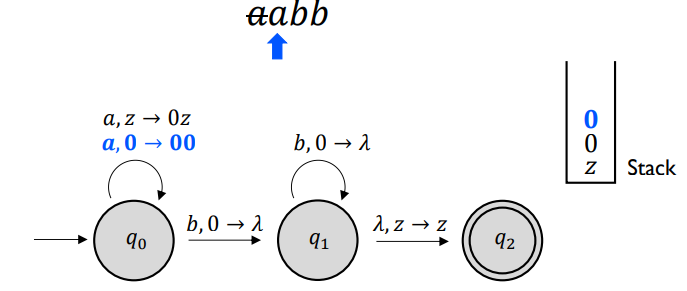



- 즉시 설명 (ID)
- PDA의 구성을 설명하는 데 사용되는 표기법
- (𝑞, 𝑤, 𝑢)로 나타냅니다.
- 𝑞: 현재 상태
- 𝑤: 입력 문자열의 남은 부분
- 𝑢: 스택 내용물 (가장 왼쪽 기호가 스택의 꼭대기를 나타냄)
- 한 ID에서 다른 ID로의 이동은 "⊢" (돌려주는 화살표) 기호로 표시됩니다.
- 예: (𝑞1, 𝑎𝑤, 𝑏𝑥) ⊢ (𝑞2, 𝑤, 𝑦𝑥)
- 즉시 설명 (ID): 예시
- "𝑎𝑎𝑏𝑏" 처리 중
- (𝑞0, 𝑎𝑎𝑏𝑏, 𝑧) ⊢ (𝑞0, 𝑎𝑏𝑏, 0𝑧) ⊢ (𝑞0, 𝑏𝑏, 00𝑧) ⊢ (𝑞1, 𝑏, 0𝑧) ⊢ (𝑞1, 𝜆, 𝑧) ⊢ (𝑞2, 𝜆, 𝑧)
- (𝑞0, 𝑎𝑎𝑏𝑏, 𝑧) ⊢ ∗ (𝑞2, 𝜆, 𝑧)
- PDA로 받아들여지는 언어
- 𝑀 = (𝑄, Σ, 𝛤, 𝛿, 𝑞0, 𝑧, 𝐹)이 비결정적 푸시다운 오토마타인 경우
- 𝑀에 의해 받아들여지는 언어는 다음과 같습니다.
- 𝐿 (𝑀) = {𝑤 ∈ Σ ∗ ∶ (𝑞0, 𝑤, 𝑧) ⊢ ∗ (𝑝, 𝜆, 𝑢) , 𝑝 ∈ 𝐹, 𝑢 ∈ Γ ∗}
- 이 언어는 𝑀을 문자열 끝에서 최종 상태로 이동시킬 수 있는 모든 문자열의 집합입니다.
- 최종 스택 내용물 𝑢는 이 정의에 대해 관계가 없습니다.
- 또 다른 예시: 𝐿 = {𝑤𝑤^𝑅: 𝑤 ∈ {𝑎, 𝑏}*} 를 위한 PDA 설계
- 𝑀 = ({𝑞0, 𝑞1, 𝑞2},{𝑎, 𝑏},{0,1, 𝑧}, 𝛿, 𝑞0, 𝑧,{𝑞2})

- Processing "𝑎𝑏𝑏𝑎"
- (𝑞0, 𝑎𝑏𝑏𝑎, 𝑧) ⊢ (𝑞0, 𝑏𝑏𝑎, 0𝑧) ⊢ (𝑞0, 𝑏𝑎, 10𝑧) ⊢ (𝑞1, 𝑏𝑎, 10𝑧) ⊢ (𝑞1, 𝑎, 0𝑧) ⊢ (𝑞1, 𝜆, 𝑧) ⊢ (𝑞2, 𝜆, 𝑧)
- 또 다른 예시: 𝐿 = {𝑤 ∈ {𝑎, 𝑏} ∗ : 𝑛𝑎( 𝑤 )= 𝑛𝑏( 𝑤 )}를 위한 PDA 설계
- 𝑀 = ({𝑞0, 𝑞1},{𝑎, 𝑏},{0,1, 𝑧}, 𝛿, 𝑞0, 𝑧,{𝑞1})

- Practice: Design a PDA for 𝐿 = {𝑎^𝑛𝑏^2𝑛: 𝑛 ≥ 0}