전공 공부/인공지능(Artificial Intelligence)

[인공지능] Constraint Satisfaction Problems - 1

7_JUN_7 2023. 10. 11. 19:18

Outline

  • Constraint Satisfaction Problems (CSPs):
    • CSPs는 여러 변수와 이러한 변수에 대한 제약 조건들 사이의 관계를 표현하는 문제이다.
  • DFS and Backtracking Search:
    • 깊이 우선 탐색(DFS) 및 백트래킹 탐색은 CSPs를 해결하는 데 사용되는 알고리즘이다. 백트래킹 탐색은 특히 제약 조건을 만족하지 않는 솔루션을 빠르게 배제하여 탐색 공간을 줄인다.
  • Speed-ups:
    • Ordering: 변수의 값을 시도하는 순서를 최적화하여 탐색 속도를 향상시킬 수 있다.
    • Filtering: 불가능한 솔루션을 조기에 감지하여 탐색 공간을 줄일 수 있다.
    • Structure: 문제의 구조를 활용하여 탐색 속도를 향상시킬 수 있다.
  • Iterative Algorithms for CSPs:
    • 반복적인 알고리즘도 CSPs를 해결하는 데 사용된다. 이러한 알고리즘은 문제를 반복적으로 해결하여 점진적으로 최적의 솔루션에 도달한다.

What is search for?

Constraint Satisfaction Problems (CSPs)의 기본 개념과 관련된 것으로, 여기서 말하는 검색이란, 에이전트가 환경 내에서 어떻게 행동하고 문제를 해결하는지에 대한 기본 가정과 원칙을 설명한다.

  • Assumptions About the World
    • 문제 해결 과정에서 고려되는 기본 가정들에 대해 설명한다.
    • 단일 에이전트( a single agent ), 결정론적 행동 ( deterministic actions ), 완전히 관찰된 상태 ( fully observed state ), 이산 상태 공간( discrete state space) 네 가지 요소가 존재 :
      • Single Agent: 이 가정에서는 환경 내에서 활동하는 단일 에이전트만 고려된다. 단일 에이전트는 환경과 독립적으로 상호작용하며, 문제를 해결하기 위해 행동한다.
      • Deterministic Actions: 에이전트의 모든 행동은 결정론적이다. 결정론적 행동이란, 주어진 상태에서 특정 행동을 수행하면 항상 동일한 결과 상태로 이어진다는 것을 의미한다. 즉, 환경의 불확실성이나 무작위성이 행동의 결과에 영향을 주지 않는다.
      • Fully Observed State: 에이전트는 환경의 현재 상태를 완전히 관찰할 수 있다. 완전히 관찰된 상태는 에이전트가 환경의 모든 정보를 알고 있으며, 이 정보를 바탕으로 행동을 계획하고 수행할 수 있다는 것을 의미한다.
      • Discrete State Space: 상태 공간은 이산적이다. 이산 상태 공간이란, 환경의 상태가 연속적이지 않고, 명확하게 구분되는 이산 값들로 표현된다는 것을 의미한다. 이를 통해 에이전트는 각 상태를 명확하게 식별하고, 상태 간의 전환을 더 쉽게 이해하고 계획할 수 있다.
    • 이러한 가정들은 Constraint Satisfaction Problems (CSPs) 문제를 모델링하고 해결할 때 문제 해결 과정을 단순화하고, 에이전트의 행동과 환경의 상태를 명확하게 이해하고 분석하는 데 도움을 준다.
  • Planning: 행동의 순서(Sequences of Actions)
    • 목표까지의 경로(path)가 중요하다. : 이 경로는 에이전트가 목표 상태에 도달하기 위해 수행해야 하는 행동의 순서를 나타낸다.
    • 경로는 다양한 비용(cost)과 깊이(depth)를 가진다. : 비용은 경로를 따라 수행되는 행동들의 총 비용을 나타내며, 깊이는 경로의 길이를 나타낸다.
    • 휴리스틱은 문제 특정 지침을 제공한다. : 이는 에이전트가 목표 상태에 더 효과적으로 도달할 수 있도록 도와준다.
  • Identification: Assignments to Variables
    • 문제 해결 과정에서 변수에 값을 할당하는 방식에 대해 설명한다.
    • 목표(goal) 자체가 중요하며, 경로(path)는 중요하지 않다.
    • 일부 공식화(formualtion)를 위해 모든 경로는 동일한 깊이를 가진다.
    • CSPs는 식별 문제(identification problem)의 특화된 클래스(specialized class)이다. 식별 문제에서는 변수에 대한 할당이 중요하며, CSPs는 이러한 유형의 문제에 특화된 형태이다.

Constraint Satisfaction Problems

Standard Search Problems :

  • State is a “black box”: 상태는 임의의 데이터 구조로 표현된다. 이때 blackbox는 상태의 내부 구조나 세부 정보에 대한 명확한 정의나 제한이 없음을 의미한다.
  • Goal Test: 목표 테스트는 상태에 대한 어떠한 함수로도 정의될 수 있다.
  • Successor Function: 후속 함수는 어떠한 형태로도 정의될 수 있다. 

Constraint Satisfaction Problems (CSPs):

  • CSPs는 검색 문제(Search Problem)의 특수한 부분 집합(Special subset)이다.
  • 상태는 변수 X_i와 도메인 D에서의 값으로 정의된다. 때로는 도메인 D가 i에 따라 다를 수 있다.
  • Goal Test: 목표 테스트는 변수의 부분 집합에 대한 허용 가능한 값 조합 (allowable combination of values)을 특정하는(specifying) 제약 조건의 집합(set of constraints)이다.

Simple Example of a Formal Representation Language

  • CSPs는 공식 표현 언어의 간단한 예시를 제공한다.

CSPs는 표준 검색 알고리즘(standard search algorithm)보다 더 강력한 일반 목적(general-purpose)의 알고리즘을 사용할 수 있게 한다.

CSP Examples

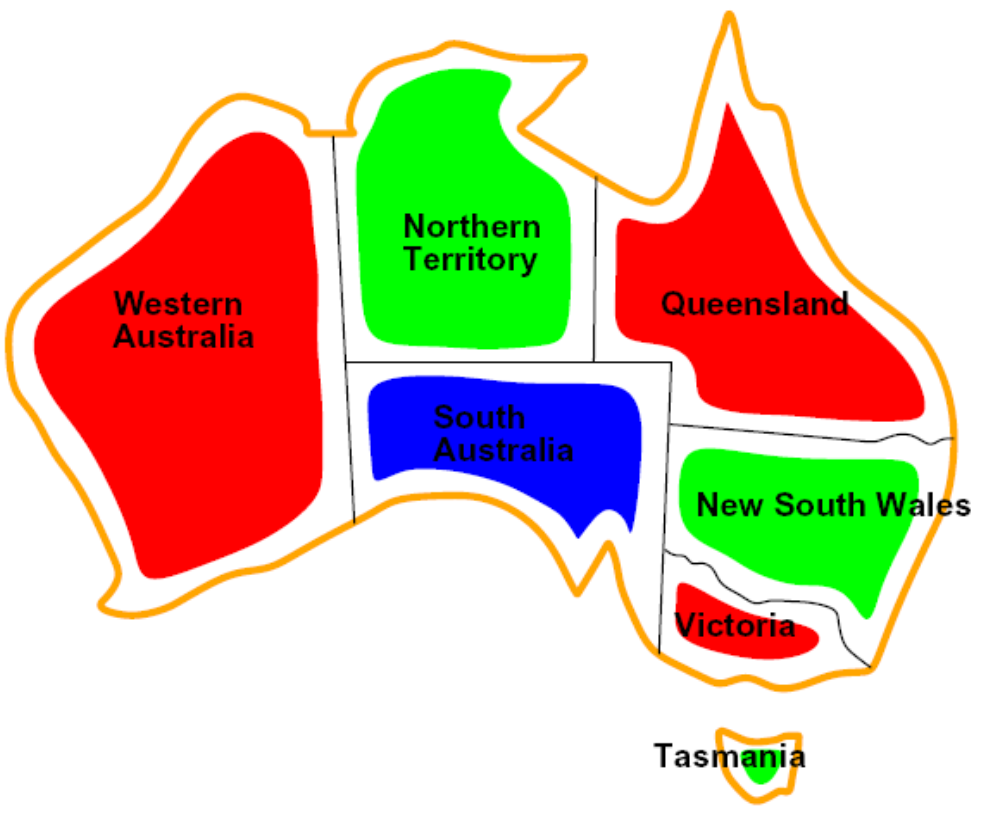
Example : Map Coloring

지도 색칠 문제는 전형적인 Constraint Satisfaction Problem (CSP)의 예시로, 각 지역 또는 국가에 색상을 할당하는 동안 특정 제약 조건을 만족시켜야 한다.

  • Variables: 지도 색칠 문제에서 변수는 각각의 지역 또는 국가를 나타낸다. 각 지역 또는 국가는 특정 색상으로 채워진다.
    • 총 7개의 변수가 존재한다 - WA, NT, Q, NSW, V , SA, T
  • Domains: 도메인은 각 지역 또는 국가에 할당할 수 있는 가능한 색상의 집합을 나타낸다. 기본적인 지도 색칠 문제에서는 주로 세 가지 색상 (빨강, 초록, 파랑)이 사용된다.
    • D={red,green,blue}
  • Constraints: 제약 조건은 인접한 지역(adjacent regions)이나 국가들이 서로 다른 색상을 가져야 한다는 것을 명시한다. 이는 인접한 지역 또는 국가가 동일한 색상으로 채워지지 않도록 해야한다.
    • 예시) 
    • 암시적 조건(implicit) : WA != NT
    • 명시적 조건 (explicit) : (WA ,NT) ∈ {(red,green),(red,blue),...}
  • Solutions: 해결책은 모든 제약 조건을 만족하는 변수 할당이다. 즉, 모든 지역 또는 국가가 색칠되어 있으며, 인접한 지역 또는 국가 사이에 동일한 색상이 없는 경우이다.
    • 예시) 
    • {WA=red , NT=green , Q=red , NSW=green, V=red, SA=blue, T=green}

Example: N-Queens

이 문제는 다양한 방식으로 공식화될 수 있으며, 두 가지 방식을 소개한다.

Formulation 1

  • Variables: X_ij
    • 이 문제에서 변수는 체스판의 각 위치를 나타낸다. 여기서 i는 column, j는 row를 나타낸다.

X_ij의 모든 합은 체스판의 위치의 개수 N과 같다.

  • Domains: {0,1}
    • 도메인은 각 위치에 할당할 수 있는 가능한 영역의 집합이다. 즉 각 위치에 퀸이 존재하거나 존재하지 않는 둘 중하나의 경우이므로 0 과 1로 표현할 수 있다.
  • Constraints:
    • 제약 조건은 퀸들이 서로 공격할 수 없도록 배치되어야 한다는 것을 명시한다. 즉, 어떤 두 퀸도 같은 행, 열 또는 대각선에 위치할 수 없다.

Constraints를 적용한 Formulation 1의 예시. 두 위치를 관측했을 때 같은 행 또는 열 또는 대각선에는 둘 중 하나에만 존재하거나 아예 존재하지 않는 상태만 허용된다.

Formulation 2

  • Variables: Q_k
    • 이 문제에서의 변수는 배치된 퀸을 나타낸다. 여기서 k는 k번째 퀸을 말한다.
  • Domains:
    • 도메인은 각 퀸이 배치될 수 있는 체스판의 행 또는 열의 번호 집합을 나타낸다. N-Queens 문제에서는 N x N 크기의 체스판이 있으므로, 각 퀸은 N개 배치가능하다. ( 한 행 또는 열당 하나의 퀸만 배치 가능하니까)
    • D = {1,2,3,...,N}
  • Constraints:
    • 제약 조건은 퀸들이 서로 공격할 수 없도록 배치되어야 한다는 것을 명시한다. 즉, 어떤 두 퀸도 같은 행, 열 또는 대각선에 위치할 수 없다.
    • Implicit( 암시적 제약 조건 ): 암시적 제약 조건은 퀸들이 서로 공격할 수 없도록(non-threatening) 하는 기본적인 규칙을 나타낸다. 즉, 어떤 i,j의 퀸도 같은 행, 열 에 위치할 수 없다

  •  
    • Explicit: 명시적 제약 조건은 문제의 특정 상황이나 조건에 따라 추가로 정의될 수 있는 제약 조건을 나타냅니다. 예를 들어, 1,2번째 행 또는 열 에 배치된 퀸을 배치할 수 있는 경우는 (1,3),(1,4?!?!?!