[계산이론] Context-Free Languages - 1

Context-Free Languages ( 문맥 무관 언어)

정규 언어가 아닌 언어들이 존재한다.

• 예를 들면, 𝐿 𝐺 = 𝑎^𝑛𝑏^𝑛 (𝑛 ≥ 0)와 같은 언어들

이러한 언어를 정의하는 다른 카테고리는 무엇인가?

• 문맥 무관 언어 (Context-Free Languages)
  • 정규 언어보다 더 넓은 범위의 언어를 생성할 수 있다.
  • 소스 코드 파싱, 프로그래밍 언어 등에서 널리 사용된다.

• 정의
  • 문맥 무관 문법은 4-튜플로 이루어져 있다: 𝐺 = (𝑉, 𝑇, 𝑆, 𝑃)
  • V: 유한한 변수 집합 (비종결 기호)
  • T: 유한한 기호 집합 (종결 기호)
  • S: 시작 변수 (𝑆는 𝑉의 원소)
  • P: 유한한 생산 규칙 집합 (𝑃는 𝑉 × (𝑉 ∪ 𝑇^∗)의 부분집합)
    • 𝑃의 모든 생산 규칙은 𝑨 → 𝒙의 형태를 가지며, 여기서 𝑨는 𝑽의 원소이고 𝒙는 𝑽 ∪ 𝑻^∗의 원소이다.
    • (정규 언어: 우측 선형): 𝑃는 𝐴 → 𝑥𝐵 | 𝑥의 형태를 가지며, 여기서 𝐴, 𝐵는 𝑉의 원소이고 𝑥는 𝑇^∗의 원소이다.
  •  언어 𝐿이 문맥 무관하다고 할 때, 그리고 그때에만 문맥 무관 문법 𝐺가 존재하여 𝐿 = 𝐿(𝐺)을 만족한다.

vs. Regular languages ( 정규 언어와 비교 )

 

 

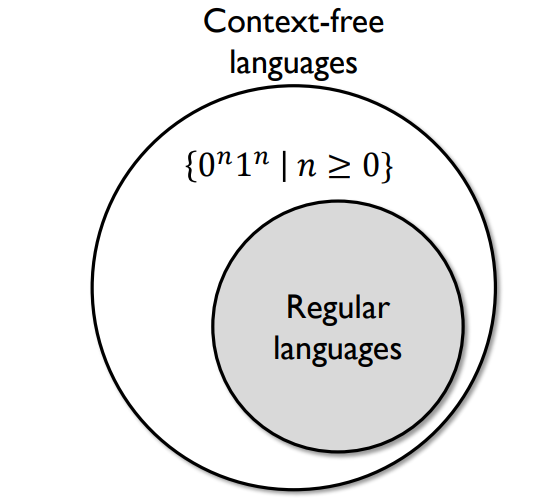
예시 문제

• 문법 𝐺 = 𝑆 , 𝑎, 𝑏 , 𝑆, 𝑃를 고려해보세요. 여기서 𝑃는 𝑆 → 𝑎𝑆𝑏 | 𝜆로 주어진다.
  • 𝑆 ⇒ 𝑎𝑆𝑏 ⇒ 𝑎𝑎𝑆𝑏𝑏 ⇒ 𝑎𝑎𝑏𝑏 (𝑆 ⇒ ∗ 𝑎𝑎𝑏𝑏)
  • 𝐿(𝐺) = {𝑎 𝑛𝑏 𝑛 | 𝑛 ≥ 0}
  • Note : 𝑆 → 𝑎𝑆𝑏, 𝑆 → 𝜆 는 𝑆 → 𝑎𝑆𝑏 | 𝜆 로 표현될 수 있습니다.

 

• 𝐺 = 𝑆 , (, ) , 𝑆, 𝑃를 고려하고 𝐿(𝐺) = {𝑤 ∈ {, , )}^∗ | 𝑤는 균형을 이룸}을 생각해보세요.
  • 𝜆, (), (()), (()()), ... ∈ 𝐿
  • (), ), )), (, ... ∉ 𝐿
  • 𝑆 → 𝑆𝑆 | (𝑆) | 𝜆

 

 

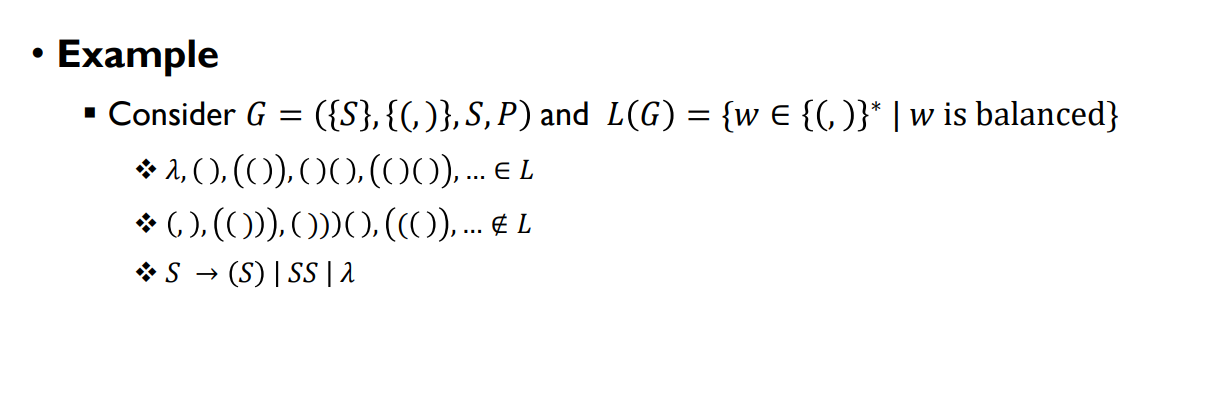
• 𝐿 = 𝑎 𝑛𝑏 2𝑛 (𝑛 ≥ 1)에 대한 문법을 찾으세요.
  • 𝑎𝑏𝑏, 𝑎𝑎𝑏𝑏𝑏𝑏, 𝑎𝑎𝑎𝑏𝑏𝑏𝑏𝑏𝑏 … 이 𝐿에 포함됩니다.
  • 𝑎𝑏, 𝑎𝑎𝑏, 𝑎𝑏𝑎𝑏𝑎 … 는 𝐿에 포함되지 않습니다.
  • 𝑆 → 𝑎𝑆𝑏𝑏 | 𝑎𝑏𝑏

 

실습문제

• 𝐿(𝐺) = {𝑤𝑤^𝑅 | 𝑤 ∈ {𝑎, 𝑏}^*}을 고려하세요.
  • 문맥-자유 문법 𝐺 = {𝑆, 𝑎, 𝑏, 𝑆, 𝑃}에서 𝑃를 찾으세요.
• 𝐿(𝐺) = {𝑎^𝑛𝑏^𝑚 | 𝑛 ≠ 𝑚}을 고려하세요.
  • 문맥-자유 문법 𝐺 = {𝑆, 𝐴, 𝐵, 𝐶, 𝑎, 𝑏, 𝑆, 𝑃}에서 𝑃를 찾으세요.

 

 

• ▪ 다음 언어가 정규적이지 않음을 보이고, CFG(문맥-자유 문법)를 찾으세요.
  • 𝐿 = {𝑤 | 𝑤 ∈ {𝑎, 𝑏}^*, 𝑛_𝑎(𝑤) = 𝑛_𝑏(𝑤)}
    • 𝑎𝑏𝑏𝑎, 𝑎𝑎𝑎𝑏𝑏𝑏, 𝑎𝑏𝑎𝑏𝑎𝑏, 𝑎𝑏𝑏𝑎𝑎𝑎𝑏𝑏 … ∈ 𝐿
    • 𝑎𝑏𝑏, 𝑎𝑎𝑏𝑏𝑏𝑎𝑎, 𝑎𝑏𝑎𝑏𝑎, … ∉ 𝐿

 

Leftmost and Rightmost derivation ( 가장 왼쪽과 가장 오른쪽 유도)

 

• 유도는 각 단계에서 가장 왼쪽(또는 가장 오른쪽)의 변수가 대체되는 경우 가장 왼쪽(또는 가장 오른쪽) 유도라고 합니다.
• 예를 들어, 다음의 생성 규칙을 가진 문법 𝐺를 고려하십시오.
  • 𝑆 → 𝑎𝐴𝐵, 𝐴 → 𝑏𝐵𝑏, 𝐵 → 𝐴 | 𝜆
  • 문자열 𝑎𝑏𝑏𝑏𝑏의 가장 왼쪽 유도는 다음과 같습니다.
    • 𝑆 ⇒ 𝑎𝐴𝐵 ⇒ 𝑎𝑏𝐵𝑏𝐵 ⇒ 𝑎𝑏𝑏𝐵 ⇒ 𝑎𝑏𝑏𝐴 ⇒ 𝑎𝑏𝑏𝑏𝐵𝑏 ⇒ 𝑎𝑏𝑏𝑏𝑏
  •  문자열 𝑎𝑏𝑏𝑏𝑏의 가장 오른쪽 유도는 다음과 같습니다.
    • 𝑆 ⇒ 𝑎𝐴𝐵 ⇒ 𝑎𝐴 ⇒ 𝑎𝑏𝐵𝑏 ⇒ 𝑎𝑏𝐴𝑏 ⇒ 𝑎𝑏𝑏𝐵𝑏𝑏 ⇒ 𝑎𝑏𝑏𝑏𝑏

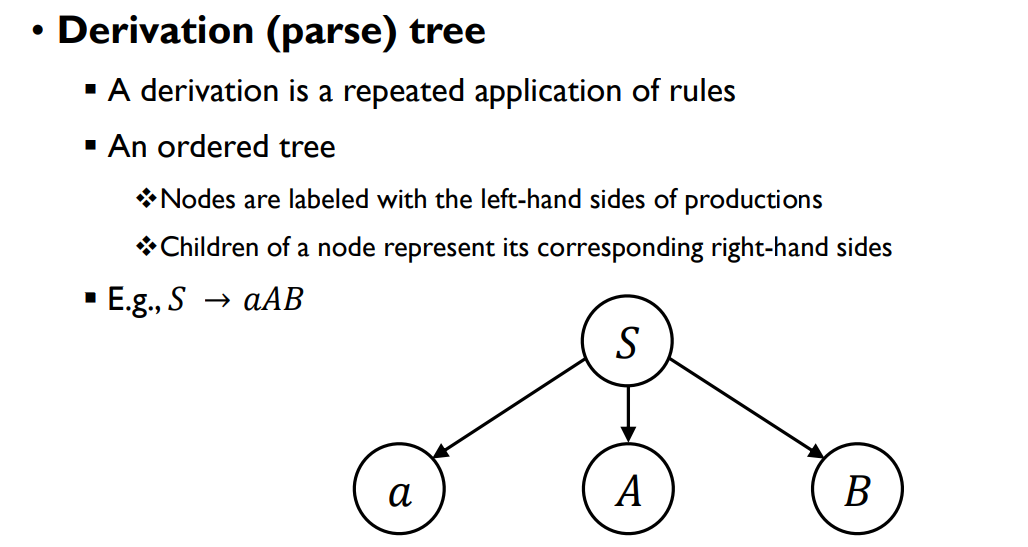
유도 (파싱parse) 트리

• 유도는 규칙의 반복적인 적용입니다.
• 순서가 지정된 트리
  • 노드는 생성규칙의 왼쪽 항목으로 레이블이 붙습니다.
  • 노드의 자식들은 해당 노드의 오른쪽 항목을 나타냅니다.
• 예를 들면, 𝑆 → 𝑎𝐴𝐵

 

예시 문제

• 생성규칙을 가진 문법 𝐺를 고려하십시오.
  • 𝑆 → 𝑎𝐴𝐵, 𝐴 → 𝑏𝐵𝑏, 𝐵 → 𝐴 | 𝜆
  • 𝑆 ⇒ 𝑎𝑨𝐵 ⇒ 𝑎𝑏𝑩𝑏𝐵 ⇒ 𝑎𝑏𝑏𝑩 ⇒ 𝑎𝑏𝑏𝑨 ⇒ 𝑎𝑏𝑏𝑏𝑩𝑏 ⇒ 𝑎𝑏𝑏𝑏𝑏
  • 이것은 유도를 나타낼 수 있지만 순서를 보여줄 수는 없습니다.