[인공지능] Markov Decision Processes I - 1
Outline
• Uncertain outcomes
MDP search tree
Value
Q-value
Value iteration
Non-Deterministic Search
Example: Grid World

미로 같은 문제
- 에이전트는 그리드 내에 존재합니다.
- 벽이 에이전트의 경로를 막습니다.
노이즈가 있는 움직임: 행동이 항상 계획대로 되지 않습니다.
- 80%의 확률로, 북쪽(North) 행동은 에이전트를 북쪽으로 이동시킵니다 (그 방향에 벽이 없는 경우).
- 10%의 확률로, 북쪽 행동은 에이전트를 서쪽(West)으로 보내고, 10%는 동쪽(East)으로 보냅니다.
- 에이전트가 이동하려는 방향에 벽이 있으면 에이전트는 움직이지 않습니다.
에이전트는 매 시간 단계마다 보상을 받습니다.
- 각 단계마다 작은 "생존" 보상이 주어집니다 (음수일 수도 있습니다).
- 큰 보상은 마지막에 주어집니다 (좋거나 나쁠 수 있습니다).
목표: 보상의 합을 최대화합니다.
Grid World Actions


Markov Decision Processes
MDP는 다음으로 정의됩니다:
- 상태 집합 𝑠 ∈ 𝑆
- 행동 집합 𝑎 ∈ 𝐴
- 전이 함수 𝑇(𝑠, 𝑎, 𝑠’)
- 𝑎가 𝑠에서 𝑠’로 이어지는 확률, 즉, 𝑃(𝑠’| 𝑠, 𝑎)
- 모델 또는 동역학이라고도 함
- 보상 함수 𝑅(𝑠, 𝑎, 𝑠’)
- 때로는 그냥 𝑅(𝑠) 또는 𝑅(𝑠’)
- 시작 상태
- 종료 상태가 있을 수 있음
MDPs는 비결정론적 검색 문제입니다.
- 그것들을 해결하는 한 가지 방법은 기대값 최대화 검색(expectimax search)을 사용하는 것입니다.
- 곧 새로운 도구를 갖게 될 것입니다.
What is Markov about MDPs?( MDPs에서의 마르코프란 무엇인가?)
"마르코프"는 일반적으로 현재 상태가 주어지면 미래와 과거가 독립적이라는 것을 의미합니다.
마르코프 결정 과정에서 "마르코프"란 행동의 결과가 오직 현재 상태에만 의존한다는 것을 의미합니다.

이것은 검색(search)과 매우 유사하며, 여기서 후속 함수는 현재 상태에만 의존할 수 있습니다 (history에는 의존하지 않습니다).
Policies
결정론적 단일 에이전트 검색 문제에서는 시작부터 목표까지의 최적의 계획 또는 행동의 연속을 원했습니다.
MDPs에서는 최적의 정책 𝜋 * : 𝑆 → 𝐴를 원합니다.
- 정책 𝜋는 각 상태에 대한 행동을 제공합니다.
- 최적(optimal)의 정책은 따르면 예상 유틸리티를 최대화하는 것입니다.
- 명시적(explicit) 정책은 reflex 에이전트를 정의합니다.
Expectimax는 전체 정책을 계산하지 않았습니다.
- 그것은 단 하나의 상태에 대한 행동만을 계산했습니다.
ex : 보물 탐색 그리드 예제에서
모든 비종료 상태 s에 대해서 R(s, a, s’) = -0.03인 경우의 최적 정책
Optimal Policies(최적 정책)

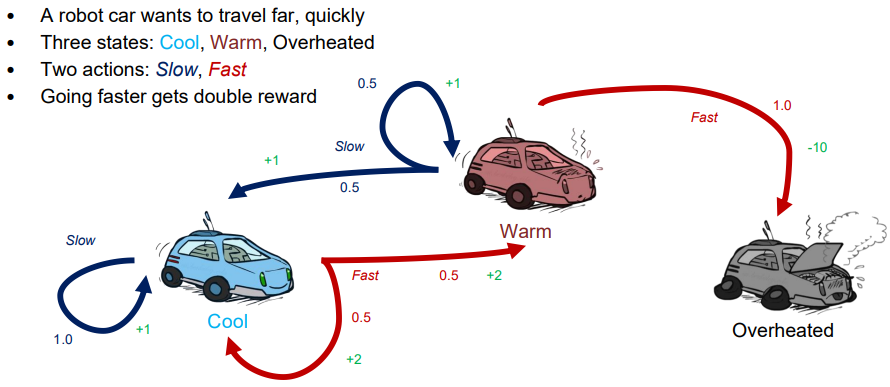
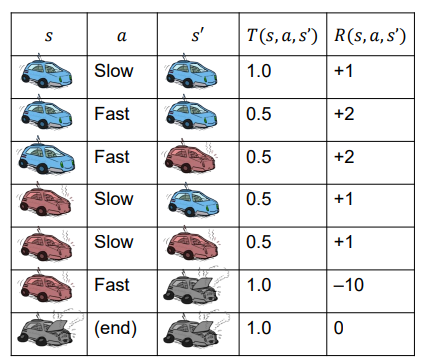
Example : Racing
- 로봇 자동차는 빠르게 멀리 가고 싶어합니다.
- 세 가지 상태: 시원한(Cool), 따뜻한(Warm), 과열된(Overheated)
- 두 가지 행동: 느린(Slow), 빠른(Fast)
- 더 빠르게 가면 두 배의 보상을 받습니다.
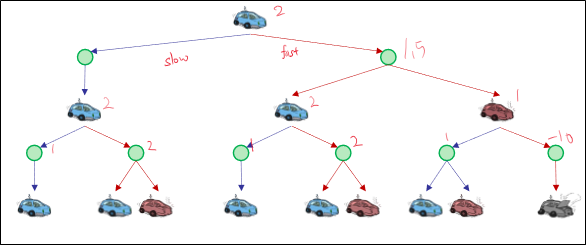
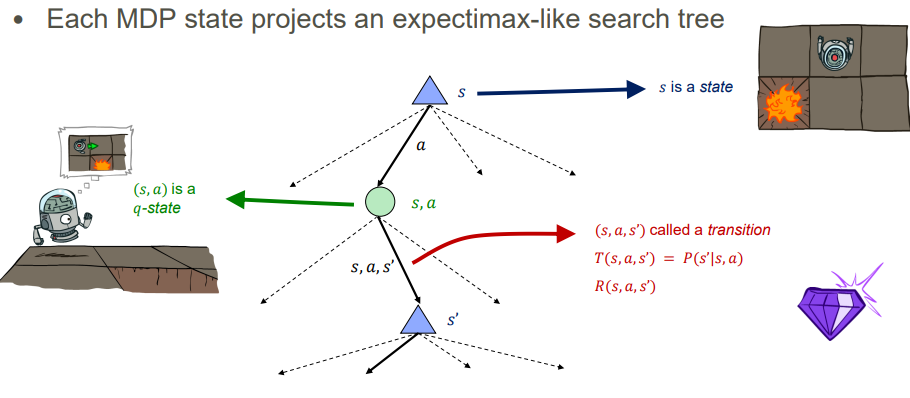
MDP Search Trees
각 MDP 상태는 expectimax와 유사한 검색 트리를 투영합니다.
Utilities of Sequences ( 시퀀스의 유틸리티)
에이전트는 보상 시퀀스에 대해 어떤 선호도를 가져야 할까요?
더 많은 것이 좋을까요, 아니면 더 적은 것이 좋을까요? [1, 2, 2] or [2, 3, 4]
지금 받을까요, 아니면 나중에 받을까요? [0, 0, 1] or [1, 0, 0]
Discounting
보상의 합을 최대화하는 것이 합리적입니다.
지금 받는 보상을 나중에 받는 보상보다 선호하는 것도 합리적입니다.
한 가지 해결책: 보상의 가치가 지수적으로(exponentially) 감소합니다.

어떻게 할인할 것인가?
- 레벨을 하나 내려갈 때마다 할인률을 한 번 곱합니다.
왜 할인하는가?
- 더 빠른 보상은 나중의 보상보다 더 높은 유틸리티를 갖는 것이 타당합니다.
- 또한 우리의 알고리즘이 수렴하는 데 도움을 줍니다.
예시: 0.5의 할인율
- U([1,2,3]) = 11 + 0.52 + 0.25*3
- U([1,2,3]) < U([3,2,1])
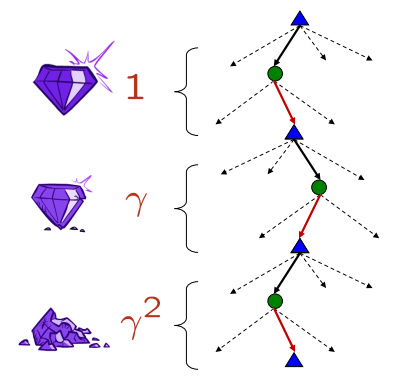
Stationary Preferences* ( 정상적인 선호도)
• 정리: 정상적인 선호도를 가정한다면:
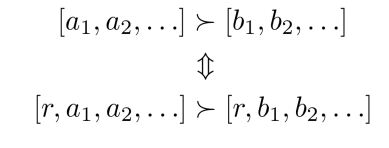
그렇다면: 유틸리티를 정의하는 두 가지 방법만 있습니다.
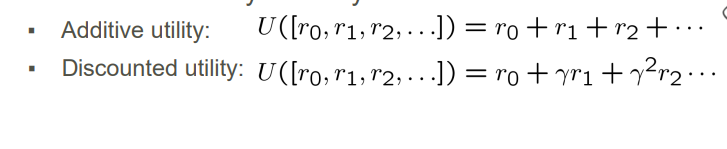
Quiz: Discounting
Given:
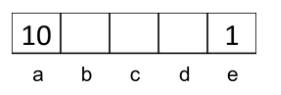
- 행동: 동쪽(East), 서쪽(West) 및 종료(Exit) (종료 상태 a, e에서만 사용 가능)
- 전이: 결정론적
퀴즈 1: 𝛾 = 1인 경우, 최적의 정책은 무엇인가요?

퀴즈 2: 𝛾 = 0.1인 경우, 최적의 정책은 무엇인가요?

퀴즈 3: 상태 d에 있을 때 서쪽(West)과 동쪽(East)이 동일하게 좋은 𝛾는 어느 것인가요?

Infinite Utilities?!
문제: 게임이 영원히 지속된다면? 우리는 무한한 보상을 받게 되는 건가?
해결책:
- 유한한 수평선(Finite horizon): ( depth-limited search 과 유사)
- 고정된 𝑇 단계 후에 에피소드를 종료합니다 (예: 생명)
- nonstationary(비정상적) 정책을 제공합니다 (𝜋는 남은 시간에 따라 달라집니다)
- 할인(Discounting): 0 < 𝛾 < 1 사용
- 더 작은 𝛾는 더 작은 "수평선"을 의미합니다 – 단기적인 초점
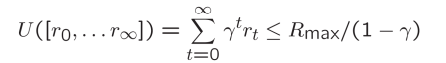
- 흡수 상태(Absorbing state): 모든 정책에 대해 종료 상태가 결국에는 도달될 것임을 보장합니다 (레이싱의 "과열된"처럼).
