[인공지능] Markov Decision Processes I - 2

Recap: Defining MDPs

• MDP는 다음과 같이 정의됩니다: ▪ 상태 집합 𝑠 ∈ 𝑆 ▪ 행동 집합 𝑎 ∈ 𝐴 ▪ 전이 함수 𝑇(𝑠, 𝑎, 𝑠’)

• 𝑎가 𝑠에서 𝑠’로 이어지는 확률, 즉, 𝑃(𝑠’| 𝑠, 𝑎)
• 이것은 모델 또는 동적 시스템이라고도 합니다. ▪ 보상 함수 𝑅(𝑠, 𝑎, 𝑠’)
• 때때로 단순히 𝑅(𝑠) 또는 𝑅(𝑠’)로 표현됩니다. ▪ 시작 상태 ▪ 종료 상태일 수도 있습니다.
•  

 

• 지금까지의 MDP 수량: ▪ 정책 = 각 상태에 대한 행동의 선택 ▪ 유틸리티 = (할인된) 보상의 합

Solving MDPs

Optimal Quantities( 최적의 수량)

 

상태 𝑠의 가치(유틸리티):

• 𝑉*(𝑠): 𝑠에서 시작하여 최적으로 행동할 때의 예상 유틸리티

q-상태(𝑠, 𝑎)의 가치(유틸리티):

• 𝑄*(𝑠, 𝑎): 상태 𝑠에서 행동 𝑎를 취한 후(그 이후에) 최적으로 행동할 때의 예상 유틸리티

최적의 정책:

• 𝜋*(𝑠) = 상태 𝑠에서의 최적 행동

Snapshot of Demo

 

Values of States( 상태의 가치)

• 기본 작업: 상태의 (expectimax) 가치 계산
  • 최적의 행동하에 있는 예상 유틸리티
  • (할인된) 보상의 평균 합계
  • 이것은 바로 expectimax가 계산한 것입니다!

 

• 값의 재귀적 정의:

Racing Search Tree

우리는 expectimax로 너무 많은 일을 하고 있습니다!

 

문제: 상태가 반복됩니다.

• 아이디어: 한 번만 필요한 수량을 계산합니다.

 

문제: 트리가 계속 진행됩니다.

• 아이디어: 변화가 작을 때까지 깊이 제한 계산을 수행하지만 깊이는 계속 증가합니다.
• 참고: 만약 γ < 1이라면 트리의 깊은 부분은 결국 중요하지 않습니다 

Computing Time-Limited Values

 

Time-Limited Values( (시간 제한 가치)

• 핵심 아이디어: 시간 제한된 가치

 

게임이 추가로 𝑘 스텝 내에 종료되면 𝑠의 최적 가치를 𝑉_𝑘(𝑠)로 정의합니다.

• 동등하게, 이것은 깊이-𝑘 expectimax가 s에서 제공할 것입니다.

Value Iteration

• 𝑉0(𝑠) = 0으로 시작: 남은 시간 단계가 없다면 예상 보상 합계는 0입니다.
• 𝑉𝑘(𝑠) 값의 벡터가 주어지면, 각 상태에서 expectimax의 한 단계를 수행합니다:

• 수렴할 때까지 반복합니다.
• 각 반복의 복잡도: 𝑂(𝑆^2𝐴)
• 정리: 고유한 최적 값으로 수렴할 것입니다.
  • 기본 아이디어: 근사치가 최적 값으로 정제됩니다.
  • 정책은 가치보다 훨씬 더 빨리 수렴할 수 있습니다.

 

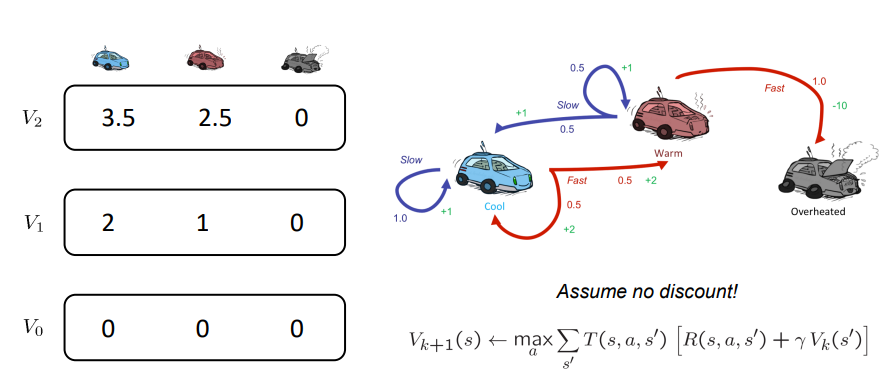
V0는 앞서 말한 것과 같이 action을 하지 않을 예정이기 때문에 0으로 초기화 되어 있다.

V1, slow는 (1.0 * (1.0 + V0 slow)와 {(0.5 * (2+V0 slow) + 0.5 * (2+V0 fast)} 를 비교,
V1, fast는 {0.5 * (1.0 + V0 slow) + 0.5 * (1.0 + V0 fast)}와 (1.5 * (-10+V0 overheat)) 를 비교,

V2 slow 는 (1.0 * (1 + 1 * V1, slow)) 와 { (0.5 * (2 + V1, slow) + 0.5 * (2 + V1, fast)} 를 비교한다.

 

Summary

• MDP는 행동의 불확실한 결과에 대한 문제를 모델링 할 수 있습니다.

 

MDP를 해결하는 것은 최적의 정책을 찾는 것입니다.

• 최적의 정책은 각 상태에서 취할 최적의 행동을 제공합니다.

행동의 결과에 대한 불확실성을 모델링하기 위해 Q-상태가 도입되었습니다.

 

상태의 가치와 q-상태의 q-가치는 재귀적으로 정의됩니다.

 

상태의 가치는 가치 반복 알고리즘을 통해 계산할 수 있습니다.