[인공지능] Markov Decision Processes II - 2
고정된 정책에 대한 유틸리티 ( Utilities for a Fixed Policy )

- 또 다른 기본 연산: 주어진 (일반적으로 최적이 아닌) 정책 하에서 상태 s의 유틸리티 계산
- 고정된 정책 𝜋에 따른 상태 𝑠의 유틸리티를 정의:
- 𝑉^𝜋 (𝑠) = s에서 시작하여 𝜋를 따라가며 예상되는 총 할인된 보상
- 재귀적 관계 (한 단계 뒤 전망(lookahead) / 벨만 방정식):

- 또 다른 기본 연산: 주어진 (일반적으로 최적이 아닌) 정책 하에서 상태 s의 유틸리티 계산: 최적이 아닌 특정 정책 하에서 상태 s의 유틸리티를 계산하는 것은 강화 학습에서 기본적인 작업 중 하나입니다.
- 고정된 정책 𝜋에 따른 상태 𝑠의 유틸리티를 정의:
- 𝑉^𝜋 (𝑠): 고정된 정책 𝜋에 따라 상태 𝑠에서 시작하여 𝜋를 따라가며 예상되는 총 할인된 보상을 나타냅니다.
- 재귀적 관계 (한 단계의 전망 / 벨만 방정식): 이 정책 하에서의 유틸리티 값은 한 단계의 전망을 반영하는 벨만 방정식을 통해 계산됩니다. 이를 통해 현재 상태의 유틸리티를 예측하고, 이를 기반으로 미래 상태의 유틸리티를 추정합니다.
Example: Policy Evaluation
- Always Go Right


- Always Go Forward


이 예시에서 정책 평가는 두 가지 다른 정책에 대해 수행됩니다.
- 항상 오른쪽으로 가기: 이 정책에서는 에이전트가 항상 오른쪽으로 움직이기 때문에 각 상태의 유틸리티를 평가할 때, 오른쪽으로 움직일 때의 보상을 고려하여 가치를 계산합니다.
- 항상 앞으로 가기: 이 정책에서는 에이전트가 항상 현재 방향으로 앞으로 움직이기 때문에 각 상태의 유틸리티를 평가할 때, 현재 방향으로 앞으로 움직일 때의 보상을 고려하여 가치를 계산합니다.
이렇게 정책 평가를 통해 얻은 가치 함수는 각 상태에서 해당 정책을 따를 때 얼마나 좋은 성능을 기대할 수 있는지를 나타내게 됩니다.
Policy Evaluation
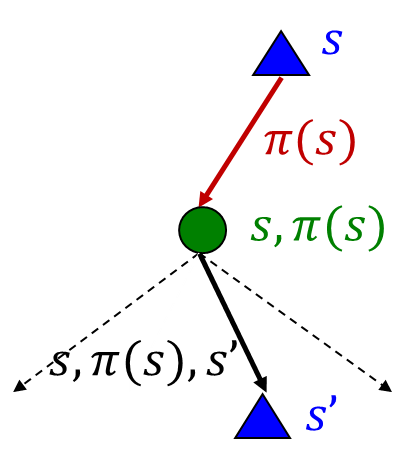
- 고정된 정책 𝜋에 대해 어떻게 𝑉 값을 계산할까요?
- 아이디어 1: 재귀적인 벨만 방정식을 업데이트로 변환하기 (가치 반복처럼)
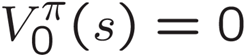
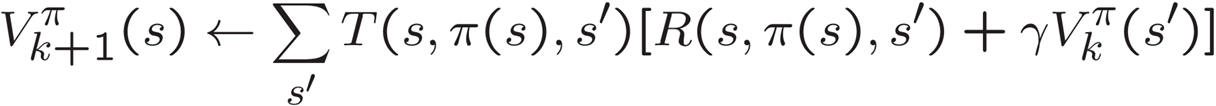
- 효율성: 각 반복마다 𝑂(𝑆^2) 복잡도
- 아이디어 2: Max가 없으면, 벨만 방정식은 선형 시스템이 됩니다.
- Matlab(또는 선호하는 선형 시스템 해결기)를 사용하여 해결
위의 문장은 정책 평가에 대한 내용과 그 효율성에 대한 두 가지 아이디어를 다루고 있습니다.
- 고정된 정책 𝜋에 대해 어떻게 𝑉 값을 계산할까요?: 특정 정책에 대해 상태 가치를 어떻게 계산할지에 대한 고민입니다.
- 아이디어 1: 재귀적인 벨만 방정식을 업데이트로 변환하기 (가치 반복처럼): 벨만 방정식을 업데이트로 변환하여 정책이 주어졌을 때 상태 가치를 계산하는 방법입니다. 이 방법은 가치 반복과 유사하게 작동하며, 각 반복에서는 상태의 가치를 업데이트하고 수렴할 때까지 반복합니다.
- 효율성: 각 반복마다 𝑂(𝑆^2) 복잡도: 아이디어 1에 따른 방법은 각 반복마다 상태의 제곱에 비례하는 복잡도를 가지게 됩니다. 즉, 계산 비용이 매우 높아집니다.
- 아이디어 2: Max가 없으면, 벨만 방정식은 선형 시스템이 됩니다.: Max가 없는 경우, 벨만 방정식은 선형 시스템으로 표현될 수 있습니다. 이 경우에는 행렬 연산을 통해 선형 시스템을 효율적으로 해결할 수 있습니다. Matlab이나 다른 선형 시스템 해결 도구를 활용하여 계산합니다.
Policy iteration
- 최적 가치에 대한 대안적인 접근 방식:
- 단계 1: 정책 평가 - 일부 고정된 정책에 대한 가치(최적이 아님!)를 수렴할 때까지 계산
- 단계 2: 정책 개선 - 수렴된(하지만 최적이 아닌) 가치를 미래 값으로 사용하여 한 단계 전망을 사용하여 정책을 업데이트
- 정책이 수렴할 때까지 단계를 반복
- 이것이 정책 반복입니다
- 여전히 최적입니다!
- 어떤 조건에서는 (훨씬) 빠르게 수렴할 수 있습니다
위의 내용은 정책 반복 알고리즘에 대한 설명과 접근 방식을 다루고 있습니다.
- 최적 가치에 대한 대안적인 접근 방식:
- 단계 1: 정책 평가: 최적이 아닌 어떤 고정된 정책에 대한 가치를 수렴할 때까지 계산합니다.
- 단계 2: 정책 개선: 수렴된 가치를 미래 값으로 사용하여 한 단계 전망을 사용하여 정책을 업데이트합니다.
- 정책이 수렴할 때까지 이러한 단계를 반복합니다.
- 이것이 정책 반복입니다:
- 여전히 최적인 정책을 찾는 방법 중 하나입니다.
- 어떤 조건에서는 가치 반복보다 (훨씬) 빠르게 수렴할 수 있습니다.
정책 반복은 최적인 정책을 찾기 위해 정책을 평가하고 개선하는 과정을 반복함으로써 동작합니다. 최적 가치에 대한 접근 방식과 달리, 정책 반복은 직접적으로 정책을 조작하여 최적의 행동을 찾아냅니다.
- 평가(Evaluation): 현재 정책 𝜋가 고정되어 있을 때, 정책 평가를 사용하여 가치를 찾습니다
- 가치가 수렴할 때까지 반복:
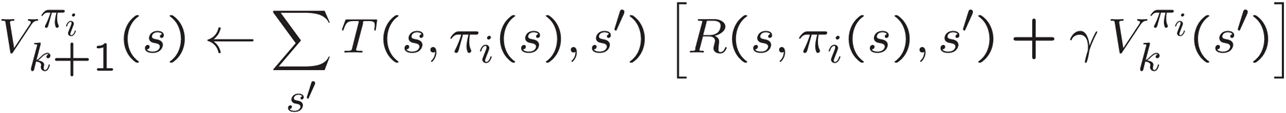
- 개선(Improvement): 고정된 가치에 대해 정책 추출을 사용하여 더 나은 정책을 얻습니다
- 한 단계 전망을 사용합니다:
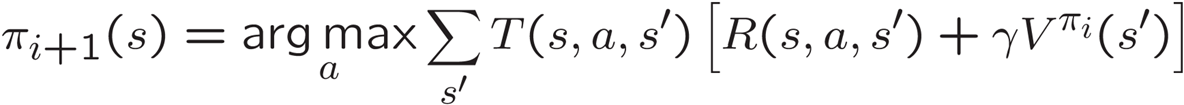
위의 내용은 정책 반복 알고리즘의 두 주요 단계에 대한 내용입니다.
- 평가(Evaluation):
- 현재 정책 𝜋가 고정되어 있을 때, 정책 평가를 사용하여 가치를 찾습니다: 주어진 정책에 대해 상태 가치를 계산합니다.
- 가치가 수렴할 때까지 반복: 정책 평가를 반복하여 가치가 수렴할 때까지 계속 수행합니다.
- 개선(Improvement):
- 고정된 가치에 대해 정책 추출을 사용하여 더 나은 정책을 얻습니다: 주어진 가치에 기반하여 현재 정책을 개선합니다.
- 한 단계 전망을 사용합니다: 미래의 상태 가치를 현재 상태의 가치로 사용하여 한 단계 앞으로 전망하여 정책을 업데이트합니다.
정책 반복은 평가와 개선 단계를 번갈아 수행하여 최적 정책을 찾아내는 알고리즘입니다. 평가는 현재 정책에 대한 가치를 찾고, 개선은 찾은 가치를 기반으로 더 나은 정책을 찾아내는 데 사용됩니다. 이를 반복함으로써 최적의 정책을 찾을 수 있습니다.
Comparison
가치 반복과 정책 반복의 비교:
가치 반복과 정책 반복은 모두 동일한 결과를 계산합니다 (모든 최적 값).
가치 반복에서:
- 각 반복마다 값과 (암묵적으로) 정책이 업데이트됩니다.
- 정책을 추적하지 않지만 액션 중 최대값을 취함으로써 암묵적으로 정책을 다시 계산합니다.
정책 반복에서:
- 고정된 정책으로 유틸리티를 업데이트하는 여러 패스를 수행합니다 (각 패스는 하나의 액션만 고려하므로 빠릅니다).
- 정책이 평가된 후 새로운 정책이 선택됩니다 (가치 반복 패스처럼 느립니다).
- 새로운 정책은 더 나아질 것입니다 (또는 완료됩니다).
둘 다 MDP(Markov Decision Process)를 해결하기 위한 동적 프로그램입니다
위의 내용은 가치 반복과 정책 반복 알고리즘의 비교에 관한 내용입니다.
- 가치 반복에서: 가치 반복은 각 반복에서 값과 (암묵적으로) 정책을 업데이트합니다. 정책은 추적되지 않지만 각 상태에서의 최대값을 찾아 암묵적으로 계산됩니다.
- 정책 반복에서: 정책 반복은 여러 패스를 통해 고정된 정책으로 유틸리티를 업데이트하며, 각 패스는 하나의 액션만을 고려하기 때문에 빠릅니다. 정책이 평가된 후, 새로운 정책을 선택하며, 이 과정은 가치 반복 패스처럼 느립니다. 그러나 이 새로운 정책은 더 나아질 것입니다.
두 알고리즘은 MDP를 해결하는 데 사용되는 동적 프로그램의 한 형태로, 최적의 정책을 찾아내기 위해 가치와 정책을 조절하고 개선하는 과정을 수행합니다.
Summary
원하는 것이 무엇인가요?
- 최적의 가치 계산: 가치 반복 또는 정책 반복 사용
- 특정 정책에 대한 가치 계산: 정책 평가 사용
- 가치를 정책으로 변환: 정책 추출 (한 단계 전망) 사용
이들은 전부 비슷해 보인다!
- 기본적으로 그렇습니다. 모두 벨만 업데이트의 변형입니다.
- 모두 한 단계 전망의 expectimax 조각을 사용합니다.
- 그들은 오직 고정된 정책을 대입하느냐, 아니면 액션 중 최대값을 찾느냐에만 차이가 있습니다.
위의 내용은 다양한 강화 학습 알고리즘들이 비슷한 구조를 가지고 있으며, 그들이 모두 벨만 업데이트의 변형이라는 공통된 특징을 갖고 있다는 점에 대한 내용입니다.
- 원하는 것이 무엇인가요?
- 최적의 가치 계산: 가치 반복이나 정책 반복을 사용합니다.
- 특정 정책에 대한 가치 계산: 정책 평가를 사용합니다.
- 가치를 정책으로 변환: 정책 추출 (한 단계 전망)을 사용합니다.
- 이들은 전부 비슷해 보이나요!
- 기본적으로 그렇습니다: 이 알고리즘들은 모두 벨만 업데이트의 변종입니다.
- 모두 한 단계 전망의 expectimax 조각을 사용합니다: 미래 예측을 통해 가치를 업데이트하는 공통된 방법을 사용합니다.
- 그들은 오직 고정된 정책을 대입하느냐, 아니면 액션 중 최대값을 찾느냐에만 차이가 있습니다: 정책이나 액션을 선택하는 방식에서 차이가 있습니다.