[인공지능] Bayesian Networks - 2
Variable Elimination: The Basic Ideas
- 가능한 한 안쪽으로 합을 이동합니다.
- 𝑃(𝐵| 𝑗, 𝑚)=𝛼∑2_(𝑒,𝑎)▒〖𝑃(𝐵)𝑃(𝑒)𝑃(𝑎|𝐵,𝑒)𝑃(𝑗|𝑎)𝑃(𝑚|𝑎)〗 =𝛼𝑃(𝐵)∑2_𝑒▒〖𝑃(𝑒)∑2_𝑎▒〖𝑃(𝑎|𝐵,𝑒)𝑃(𝑗|𝑎)𝑃(𝑚|𝑎)〗〗
- 내부에서부터 계산을 수행합니다.
- 즉, 먼저 𝑎에 대한 합을 계산하고, 그 다음에 𝑒에 대한 합을 계산합니다.
- 문제: 𝑃(𝑎|𝐵,𝑒)는 하나의 숫자가 아니라, 𝐵와 𝑒의 값에 따라 다른 숫자들의 모음입니다.
- 해결책: 이를 다차원 배열로 사용하고, 적절한 연산을 수행합니다. 이러한 배열은 "팩터(factors)"라고 불리며, 다양한 차원을 가진 숫자들의 모음을 나타냅니다.
변수 제거(Variable Elimination)는 확률 그래프 모델(Probabilistic Graphical Models)에서 추론을 수행하기 위한 중요한 기법 중 하나입니다. 이 방법은 복잡한 확률 계산을 단순화하여 효율적으로 수행하는 데 사용됩니다. 아래에서 이 방법의 기본 아이디어를 설명하겠습니다.
- 안쪽으로 합을 이동합니다: 주어진 확률식에서 가능한 한 많은 합을 내부로 이동합니다. 이것은 합산 기호(Σ)를 더 안쪽으로 옮겨서 계산을 단순화하는 것을 의미합니다. 예를 들어, 𝑃(𝐵| 𝑗, 𝑚)의 식을 보면, 합을 내부로 이동하여 𝑃(𝑒)와 𝑃(𝑎|𝐵,𝑒)𝑃(𝑗|𝑎)𝑃(𝑚|𝑎)를 별도로 계산할 수 있습니다.
- 계산은 안에서부터 밖으로 수행합니다: 이전 단계에서 합을 내부로 이동했으므로 이제 안쪽에서부터 계산을 수행합니다. 즉, 먼저 𝑎에 대한 합을 계산하고, 그 다음에는 𝑒에 대한 합을 계산합니다.
- 다차원 배열인 팩터를 사용합니다: 확률 계산을 단순화하고 숫자들의 모임을 나타내기 위해 다차원 배열을 사용합니다. 이러한 배열은 팩터라고 불리며, 여러 차원을 가진 숫자들의 모음입니다. 이 팩터를 사용하여 확률 계산을 효율적으로 수행할 수 있습니다.
변수 제거를 사용하면 확률적 그래프 모델에서 정확한 추론을 수행하는 데 도움이 되며, 중복된 계산을 피하고 계산 비용을 줄일 수 있습니다. 팩터를 사용하여 다양한 확률 변수 간의 조건부 확률을 저장하고 연산을 수행하여 베이즈 네트워크나 마르코프 랜덤 필드와 같은 모델에서 확률 추론을 최적화하는 데 사용됩니다.
Factor Zoo I ( 팩터 종류 I)
- 조인 분포(Joint distribution): 𝑃(𝑋,𝑌)
- 모든 𝑥, 𝑦에 대한 항목인 𝑃(𝑥,𝑦)
- |𝑋|×|𝑌| 행렬
- 합계가 1이 됨
- 프로젝트된 조인(Projected joint): 𝑃(𝑥,𝑌)
- 조인 분포의 일부분
- 한 𝑥에 대한 모든 𝑦에 대한 항목인 𝑃(𝑥,𝑦)
- |𝑌| 요소의 벡터
- 합계가 𝑃(𝑥)가 됨
변수의 수(대문자) = 표의 차원입니다.
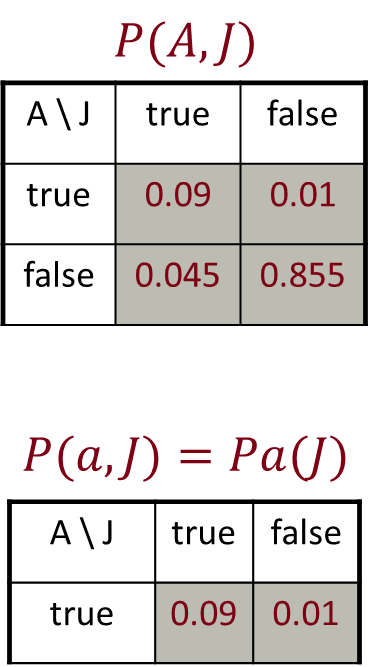
이 문장은 확률적 그래피컬 모델(Probabilistic Graphical Models)에서 사용되는 "팩터(Factor)"라고 불리는 개념에 관한 것입니다. 이 개념은 확률 분포를 표현하고 조작하는 데 사용됩니다.
- 조인 분포(Joint Distribution): 이것은 확률 변수 X와 Y의 결합 확률 분포를 나타냅니다. 이 확률 분포에는 모든 X와 Y 값에 대한 확률이 포함되어 있으며, 이를 모든 가능한 (X, Y) 조합에 대한 확률을 포함하는 행렬로 생각할 수 있습니다. 이 분포의 합은 항상 1입니다.
- 프로젝트된 조인(Projected Joint): 이것은 조인 분포의 일부를 나타냅니다. 특정한 X 값에 대한 모든 가능한 Y 값에 대한 확률을 나타내는 벡터입니다. 이 벡터는 특정한 X 값에 대한 조건부 확률 분포를 나타내며, 이 벡터의 합은 X에 대한 확률로 정규화됩니다.
이것은 확률적 그래피컬 모델에서 변수의 관계와 조건부 확률을 나타내는 데 사용되며, 조건부 독립성 및 추론과 관련된 다양한 작업에 활용됩니다. 이러한 팩터는 확률적 그래프 모델의 핵심 구성 요소 중 하나이며, 이러한 팩터를 적절하게 조작하여 확률적 모델을 이해하고 활용할 수 있습니다.
Factor Zoo II (팩터 종류 II)
- 단일 조건부(Conditional): 𝑃(𝑌 | 𝑥)
- 고정된 𝑥에 대한 모든 𝑦에 대한 항목인 𝑃(𝑦|𝑥)
- 합계가 1이 됨

- 조건부 패밀리(Family of Conditionals): 𝑃(𝑋 |𝑌)
- 다중 조건부
- 모든 𝑥, 𝑦에 대한 항목인 𝑃(𝑥|𝑦)
- 합계가 |𝑌|가 됨

이 문장은 확률적 그래피컬 모델(Probabilistic Graphical Models)에서 사용되는 "팩터(Factor)"의 두 가지 주요 유형을 설명하고 있습니다.
- 단일 조건부(Conditional): 이것은 확률 변수 Y의 조건부 확률 분포를 나타냅니다. 특정한 X 값에 대한 조건 하에서 Y의 모든 가능한 값에 대한 확률을 나타내는 분포입니다. 이 분포의 합은 항상 1이 됩니다. 이러한 조건부 분포는 특정한 조건에서 Y의 확률 분포를 표현하는 데 사용됩니다.
- 조건부 패밀리(Family of Conditionals): 이것은 다중 조건부 확률 분포의 집합을 나타냅니다. Y에 대한 여러 조건부 확률 분포가 포함되어 있으며, 이러한 분포는 모든 가능한 X와 Y 값에 대한 확률을 나타내는 것이 특징입니다. 이러한 조건부 분포의 합은 Y의 가능한 값의 수인 |𝑌|가 됩니다.
이러한 조건부 확률 분포 및 팩터는 확률적 그래피컬 모델에서 변수 간의 관계를 모델링하고 조건부 독립성을 표현하는 데 사용됩니다. 단일 조건부는 주어진 조건 하에서 특정 변수의 분포를 나타내며, 조건부 패밀리는 여러 조건 하에서 변수 간의 관계를 표현합니다. 이러한 팩터들은 확률 모델을 구성하고 추론 작업을 수행하는 데 중요한 역할을 합니다.
Operation 1: Pointwise Product( 연산 1: 요소별 곱셈 )
연산 1: 요소별 곱셈
- 첫 번째 기본 연산: 팩터들의 요소별 곱셈 (행렬 곱셈이 아닌 데이터베이스 조인과 유사함!)
- 새로운 팩터는 두 원본 팩터의 변수를 합친 것을 가지고 있음
- 각 항목은 원본 팩터에서 해당하는 항목들의 곱셈입니다.
- 예시: 𝑃(𝐽│𝐴)×𝑃(𝐴)=𝑃(𝐴,𝐽)

"요소별 곱셈(Pointwise Product)"은 확률적 그래피컬 모델에서 팩터(Factor) 간에 수행되는 기본적인 연산 중 하나입니다. 이 연산은 데이터베이스 조인과 유사하며, 두 개의 팩터를 곱하여 새로운 팩터를 생성합니다.
요소별 곱셈의 주요 특징은 다음과 같습니다:
- 새로운 팩터의 변수: 요소별 곱셈을 수행한 결과로 얻은 새로운 팩터는 두 원본 팩터의 변수를 합친 변수를 가지고 있습니다. 즉, 두 팩터의 변수 집합의 합집합이 새로운 팩터의 변수 집합이 됩니다.
- 항목별 곱셈: 새로운 팩터의 각 항목은 원본 팩터에서 해당하는 항목들의 곱셈으로 계산됩니다. 즉, 두 팩터에서 동일한 변수를 가진 항목끼리 곱셈을 수행합니다.
예를 들어, "𝑃(𝐽│𝐴)×𝑃(𝐴)=𝑃(𝐴,𝐽)"라는 예시에서는 확률 변수 A와 J에 대한 두 개의 팩터를 요소별로 곱하여 새로운 팩터 P(A, J)를 얻습니다. 이 새로운 팩터는 변수 A와 J를 모두 포함하게 됩니다.
요소별 곱셈은 확률적 그래피컬 모델에서 조건부 확률을 계산하거나 추론을 수행하는 데 사용됩니다. 두 확률 분포를 결합하거나 조건부로 다른 확률 분포를 계산할 때 유용합니다.
Example: Making Larger Factors
- 예시: P(A,J)×P(A,M)=P(A,J,M)

설명 나중에 추가
- 예시: 𝑃(𝑈,𝑉)×𝑃(𝑉,𝑊)×𝑃(𝑊,𝑋)=𝑃(𝑈,𝑉,𝑊,𝑋)
- 크기: [10,10]×[10,10]×[10,10]=[10,10,10,10]
- 즉, 300개의 숫자가 10,000개의 숫자로 확장됩니다!
- 팩터 확장은 변수 제거(Variable Elimination)를 매우 비용이 많이 들게 만들 수 있습니다.
이 예시는 확률적 그래피컬 모델에서 팩터(Factor)의 크기가 어떻게 늘어날 수 있는지를 설명합니다.
먼저, 우리는 세 개의 확률 변수 U, V, W, X에 대한 세 개의 팩터를 고려합니다: 𝑃(𝑈,𝑉), 𝑃(𝑉,𝑊), 𝑃(𝑊,𝑋). 각 팩터는 2개의 변수를 가지고 있으며, 각각의 크기는 [10, 10]입니다.
이러한 세 개의 팩터를 곱하면 하나의 큰 팩터인 𝑃(𝑈,𝑉,𝑊,𝑋)가 생성됩니다. 이 팩터의 크기는 [10, 10, 10, 10]입니다. 즉, 각 변수에 대한 10개의 가능한 값이 있으므로, 총 10,000개의 항목을 가지고 있는 팩터가 생성됩니다.
이것은 팩터 크기가 어떻게 급격하게 증가할 수 있는지를 보여주는 예시입니다. 팩터의 크기가 증가하면 변수 제거(Variable Elimination)와 같은 확률 추론 작업이 매우 비용이 많이 들게 됩니다. 따라서 모델을 효율적으로 관리하고 추론을 수행하기 위해서는 팩터 크기의 폭발을 효과적으로 다루는 방법을 고려해야 합니다.
Operation 2: Summing Out a Variable (변수제거)
두 번째 기본 연산: 팩터에서 변수를 합산(또는 제거)하는 작업
- 팩터를 더 작은 팩터로 줄입니다.
- 예시: ∑2_𝑗▒〖𝑃(𝐴,𝐽)=𝑃(𝐴,𝑗)+𝑃(𝐴,¬𝑗)=𝑃(𝐴)〗

"변수 제거(Variable Elimination)"의 두 번째 기본 연산인 "Summing Out" 또는 "변수 제거"는 확률적 그래피컬 모델에서 팩터(Factor)를 단순화하는 데 사용되는 연산입니다. 이 연산은 팩터에서 특정 변수를 합산하거나 제거하여 새로운 팩터를 생성합니다.
연산의 주요 특징은 다음과 같습니다:
- 팩터 축소: 변수 제거 연산은 주어진 팩터를 더 작은 팩터로 축소합니다. 이때 선택한 변수를 제거하고 나머지 변수들만을 포함하는 팩터를 생성합니다.
예를 들어, "∑2_𝑗▒〖𝑃(𝐴,𝐽)=𝑃(𝐴,𝑗)+𝑃(𝐴,¬𝑗)=𝑃(𝐴)〗"라는 예시에서는 변수 J를 제거하여 팩터 P(A, J)를 P(A)로 축소합니다. 이렇게 하면 변수 J가 없는 P(A) 팩터가 생성됩니다.
변수 제거 연산은 확률적 그래피컬 모델에서 조건부 확률을 계산하거나 추론을 수행하는 데 사용됩니다. 특정 변수를 제거하여 모델을 단순화하고 효율적인 확률 추론을 가능하게 합니다.
Summing Out from a Product of Factors ( 팩터의 곱으로부터 합산하기)
팩터의 곱으로부터 합산하기
- 먼저 팩터를 각각의 방향으로 프로젝션한 다음 곱을 합산합니다.
- 예시:
- ∑2_𝑎▒〖𝑃(𝑎│𝐵,𝑒)𝑃(𝑗│𝑎)𝑃(𝑚|𝑎)〗 =𝑃(𝑎│𝐵,𝑒)𝑃(𝑗│𝑎)𝑃(𝑚|𝑎)+𝑃(¬𝑎|𝐵,𝑒)𝑃(𝑗|¬𝑎)𝑃(𝑚|¬𝑎)
"팩터의 곱으로부터 합산하기"는 확률적 그래피컬 모델에서 조건부 확률을 계산하는 과정 중 하나입니다. 이 과정에서 두 개의 팩터를 곱한 다음 특정 변수에 대한 합을 수행합니다.
이 과정은 다음과 같이 진행됩니다:
- 먼저, 두 개의 팩터를 곱셈합니다. 예시에서는 𝑃(𝑎│𝐵,𝑒), 𝑃(𝑗│𝑎), 𝑃(𝑚|𝑎)의 곱을 계산합니다.
- 그 다음, 특정 변수(예시에서는 𝑎)에 대한 합을 수행합니다. 이를 위해 모든 가능한 변수 값에 대해 해당 변수 값을 적용한 후, 합을 계산합니다. 예시에서는 ∑2_𝑎▒〖𝑃(𝑎│𝐵,𝑒)𝑃(𝑗│𝑎)𝑃(𝑚|𝑎)〗를 계산하는 것입니다.
- 합산된 결과는 두 가지 항목으로 나눠집니다. 첫 번째 항목은 해당 변수(예시에서는 𝑎)의 값이 참일 때의 결과이며, 두 번째 항목은 해당 변수의 값이 거짓일 때의 결과입니다. 이러한 합산은 조건부 확률을 계산할 때 유용하며, 조건부 확률을 구성하는데 사용됩니다.
예시에서는 𝑎에 대한 합산을 수행한 결과를 통해 조건부 확률을 계산하고 있습니다. 이 과정을 통해 변수에 대한 조건부 확률을 효과적으로 계산할 수 있습니다.
Variable Elimination
- 질의(Query): 𝑃(𝑄|𝐸_1=𝑒_1,…, 𝐸_𝑘=𝑒_𝑘)
- 초기 팩터로 시작:
- 지역 조건부 확률 표(CPTs), 다만 증거로 인스턴스화됨
- 아직 숨겨진 변수(hidden variables)가 있는 경우 (𝑄 또는 증거가 아닌 경우):
- 숨겨진 변수 𝐻_𝑗를 선택
- 모든 𝐻_𝑗를 언급하는 모든 팩터의 곱에서 𝐻_𝑗를 제거(합산)
- 남은 모든 팩터를 결합하고 정규화
"변수 제거(Variable Elimination)"는 확률적 그래피컬 모델에서 확률 추론을 수행하는 고급 기술 중 하나입니다. 이 기술은 주어진 증거(evidence)와 질의(Query)를 기반으로 확률 분포를 계산하는 데 사용됩니다. 다음은 변수 제거 알고리즘의 주요 단계와 설명입니다:
- 초기 팩터 설정: 알고리즘은 초기 팩터를 설정합니다. 이러한 초기 팩터는 지역 조건부 확률 표(CPTs)와 같은 확률 모델의 구성 요소입니다. 그러나 이러한 초기 팩터는 주어진 증거에 따라 인스턴스화됩니다. 이것은 주어진 조건에서 유효한 확률 분포를 나타내는데 사용됩니다.
- 숨겨진 변수 제거: 아직 숨겨진 변수(hidden variables)가 남아 있는 경우, 알고리즘은 하나의 숨겨진 변수를 선택합니다(예: 𝐻_𝑗). 이 변수를 선택한 후, 해당 변수를 언급하는 모든 팩터의 곱에서 해당 변수를 제거합니다. 이는 숨겨진 변수를 합산(또는 제거)하는 것을 의미합니다.
- 남은 팩터 결합: 숨겨진 변수를 제거한 후, 모든 남은 팩터(숨겨진 변수가 없는)를 결합하여 하나의 큰 팩터를 생성합니다.
- 정규화: 마지막으로, 결합된 팩터를 정규화하여 확률 분포를 얻습니다. 이것은 질의(Query)에 대한 확률 분포를 나타내며, 원하는 조건부 확률 분포를 얻는 데 사용됩니다.
변수 제거는 확률적 그래피컬 모델에서 효율적인 확률 추론을 수행하는 중요한 방법 중 하나입니다. 숨겨진 변수를 제거하여 모델의 단순화와 정규화를 도와주므로, 다양한 추론 작업을 효율적으로 처리할 수 있습니다.
Example


설명 나중에 추가

설명 나중에 추가
Order Matters

- 항목 𝑍, 𝐴, 𝐵, 𝐶, 𝐷를 순서대로 정렬합니다.
- 𝑃(𝐷)=𝛼∑2_(𝑧,𝑎,𝑏,𝑐)▒〖𝑃(𝑧)𝑃(𝑎|𝑧)𝑃(𝑏|𝑧)𝑃(𝑐|𝑧)𝑃(𝐷|𝑧)〗 =𝛼∑2_𝑧▒〖𝑃(𝑧)∑2_𝑎▒〖𝑃(𝑎|𝑧)∑2_𝑏▒〖𝑃(𝑏|𝑧)〗〗 ∑2_𝑐▒〖𝑃(𝑐|𝑧)𝑃(𝐷|𝑧)〗〗
- 가장 큰 팩터는 2개의 변수(𝐷,𝑍)를 가집니다.
- 항목 𝐴, 𝐵, 𝐶, 𝐷, 𝑍를 순서대로 정렬합니다.
- 𝑃(𝐷)=𝛼∑2_(𝑎,𝑏,𝑐,𝑧)▒〖𝑃(𝑎|𝑧)𝑃(𝑏|𝑧)𝑃(𝑐|𝑧)𝑃(𝐷|𝑧)𝑃(𝑧)〗 =𝛼∑2_𝑎▒∑2_𝑏▒∑2_𝑘▒∑2_𝑧▒〖𝑃(𝑎|𝑧)𝑃(𝑏|𝑧)𝑃(𝑐|𝑧)𝑃(𝐷|𝑧)𝑃(𝑧)〗
- 가장 큰 팩터는 4개의 변수(𝐴,𝐵,𝐶,𝐷)를 가집니다.
- 일반적으로, 𝑛개의 리프(leaf)를 가질 때 팩터의 크기는 2^𝑛입니다.
"순서의 중요성(Order Matters)"는 확률적 그래피컬 모델에서 변수를 제거하는 과정에서 어떻게 순서를 선택하는지에 대한 개념입니다. 변수를 제거하는 순서가 확률 추론의 효율성과 결과에 영향을 미칠 수 있습니다.
두 가지 서로 다른 순서를 예로 들어 설명하겠습니다:
- 𝑍, 𝐴, 𝐵, 𝐶, 𝐷 순서: 이 순서로 변수를 제거할 때, 최종적으로 얻게 되는 가장 큰 팩터는 2개의 변수(𝐷, 𝑍)만을 포함하게 됩니다. 이는 팩터의 크기가 비교적 작아집니다.
- 𝐴, 𝐵, 𝐶, 𝐷, 𝑍 순서: 이 순서로 변수를 제거할 때, 최종적으로 얻게 되는 가장 큰 팩터는 4개의 변수(𝐴, 𝐵, 𝐶, 𝐷)를 포함하게 됩니다. 이 경우 팩터의 크기가 상대적으로 크게 늘어납니다.
일반적으로, 변수 제거 알고리즘에서 변수를 어떤 순서로 제거하느냐에 따라서 최종적으로 생성되는 팩터의 크기가 달라질 수 있습니다. 팩터의 크기가 크면 확률 추론이 더 복잡해지고 느려질 수 있습니다. 따라서 효율적인 변수 제거 순서를 선택하는 것은 확률 추론 성능을 향상시키는 중요한 요소 중 하나입니다.
Example Bayes’ Net: Car Insurance ce
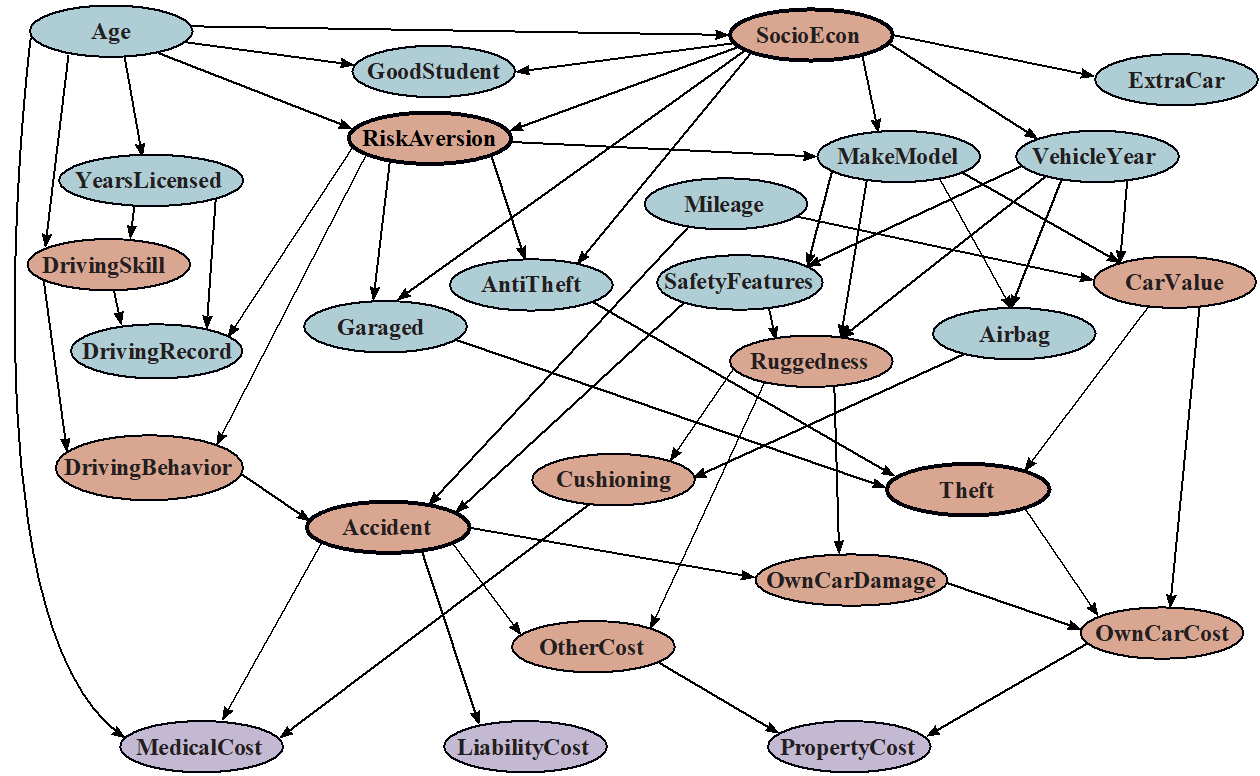
- 열거(Enumeration): 2.27억 번의 연산
- 제거(Elimination): 22.1만 번의 연산
이 예시에서는 자동차 보험에 관련된 베이즈 네트워크를 고려합니다. 이 베이즈 네트워크를 사용하여 확률 추론 작업을 수행할 때, 두 가지 다른 추론 방법을 고려하고 있습니다.
- 열거(Enumeration): 이 방법은 확률 분포를 계산하기 위해 모든 가능한 조합을 열거하는 방식을 사용합니다. 이 경우, 2.27억 번의 연산이 필요하다고 합니다. 즉, 매우 많은 계산이 필요하며, 큰 계산 비용이 발생합니다.
- 제거(Elimination): 이 방법은 변수 제거 알고리즘을 사용하여 확률 분포를 계산합니다. 이 경우, 22.1만 번의 연산만 필요하다고 합니다. 변수 제거를 사용하면 훨씬 더 효율적으로 확률 분포를 계산할 수 있으며, 연산 비용이 낮아집니다.
이러한 비교를 통해 변수 제거 알고리즘이 대규모 확률 추론 작업에서 효율적인 방법임을 확인할 수 있습니다. 열거 방법은 연산량이 훨씬 많아서 처리하기 어려울 수 있지만, 제거 방법은 효율적으로 작업을 수행할 수 있는 방법을 제공합니다.
Computational and Space Complexity
- 변수 제거의 계산 및 공간 복잡도는 가장 큰 팩터(factor)에 의해 결정됩니다 (그리고 공간이 주요 복잡도 요인입니다).
- 제거 순서는 가장 큰 팩터의 크기에 큰 영향을 미칠 수 있습니다.
- 예: ZABCD 예제에서 2^𝑛 대비 2의 크기 차이
- 항상 작은 팩터만 생성되는 순서가 항상 존재할까요?
- 아닙니다!
"계산 및 공간 복잡도(Computational and Space Complexity)"에 대한 설명은 다음과 같습니다:
- 변수 제거(Variable Elimination) 알고리즘의 계산 및 공간 복잡도는 가장 큰 팩터(factor)에 의해 결정됩니다. 이 말은 변수 제거 과정에서 생성되는 가장 큰 확률 분포 팩터가 알고리즘의 성능과 비용에 큰 영향을 미친다는 것을 의미합니다. 일반적으로 큰 팩터를 처리하는 것은 계산 및 메모리 공간 측면에서 비용이 많이 들 수 있습니다.
- 변수 제거에서 가장 큰 팩터의 크기는 제거 순서에 따라 크게 달라질 수 있습니다. 즉, 어떤 변수를 어떤 순서로 제거하느냐에 따라 최종적으로 생성되는 팩터의 크기가 결정됩니다. 예를 들어, ZABCD 예제에서 제거 순서에 따라 팩터의 크기가 2^𝑛 대비 2로 크게 달라집니다.
- 그러나 중요한 점은 항상 작은 팩터만 생성되는 순서가 항상 존재하는 것은 아니라는 것입니다. 즉, 어떤 경우에는 큰 팩터를 생성할 수밖에 없고, 이로 인해 계산 및 메모리 복잡도가 증가할 수 있습니다. 따라서 변수 제거의 성능을 최적화하려면 적절한 제거 순서를 선택하는 것이 중요합니다.
Worst Case Complexity? Reduction from SAT

- 변수: 𝑊, 𝑋, 𝑌, 𝑍
- CNF 절(clauses):
- 𝐶_1=𝑊∨𝑋∨𝑌
- 𝐶_2=𝑌∨𝑍∨¬𝑊
- 𝐶_3=𝑋∨𝑌∨¬𝑍
- 문장 𝑆= 𝐶_1∧𝐶_2∧𝐶_3
- 𝑃(𝑆)>0 이면 𝑆가 만족 가능(satisfiable)한 경우 => NP-hard
- 𝑃(𝑆)=𝐾×〖0.5〗^𝑛, 여기서 𝐾는 절(clauses)을 만족시키는 할당(assignments)의 수 => #P-hard
"최악의 경우 복잡도? SAT로의 축소"에 대한 설명은 다음과 같습니다:
- 주어진 변수 집합과 CNF(clause normal form) 형식의 논리 식을 고려합니다. 이 변수들은 𝑊, 𝑋, 𝑌, 𝑍로 표시됩니다.
- CNF 절(clauses)은 다음과 같이 정의됩니다:
- 𝐶_1=𝑊∨𝑋∨𝑌
- 𝐶_2=𝑌∨𝑍∨¬𝑊
- 𝐶_3=𝑋∨𝑌∨¬𝑍
- 이러한 CNF 절을 조합하여 문장 𝑆을 생성합니다: 𝑆= 𝐶_1∧𝐶_2∧𝐶_3
- 이 문장 𝑆이 만족 가능(satisfiable)한 경우, 이는 SAT(만족 가능성 문제, Satisfiability Problem)의 인스턴스로 간주할 수 있습니다. 이 문제는 NP-hard로 알려져 있습니다. 즉, 만족 가능한 해를 찾는 것이 어렵다는 것을 의미합니다.
- 문장 𝑆이 만족 가능한지 확인하려면 모든 가능한 할당(assignments)을 검사해야 합니다. 이 때, 𝑆이 만족되는 할당의 수를 𝐾로 표시합니다.
- 이 경우, 𝑃(𝑆)=𝐾×〖0.5〗^𝑛이며, 여기서 𝑛은 변수의 개수를 나타냅니다. 이 값은 SAT 문제의 해의 개수를 계산하는 어려운 문제인 #P-hard 문제를 다루는데 사용됩니다.
즉, 이 예시에서 언급된 문제는 SAT 문제와 그 해의 개수를 계산하는 #P-hard 문제와 관련이 있으며, 이러한 문제들은 복잡한 계산 문제로 알려져 있습니다.
Polytrees( 다형트리)
- 다형트리(Polytree)는 방향 그래프로, 비순환적인 사이클이 없는 구조를 가집니다.
- 다형트리의 경우, 네트워크 크기에 대한 변수 제거의 복잡도는 잎(leaf)에서 루트로 진행하면 선형(linear)입니다.
다형트리(Polytree)는 방향 그래프의 한 형태로, 그래프 내에 순환 사이클(cycle)이 없는 특별한 형태의 그래프를 나타냅니다. 다형트리는 그래프 이론에서 중요한 역할을 하며, 확률적 그래피컬 모델에서도 종종 사용됩니다.
다형트리의 중요한 특성 중 하나는 변수 제거(Variable Elimination)와 관련이 있습니다. 변수 제거는 확률적 그래피컬 모델에서 확률 분포를 계산하는 데 사용되는 중요한 알고리즘 중 하나입니다. 다형트리의 경우, 변수 제거 연산의 복잡도가 선형으로 유지됩니다. 이것은 변수 제거를 모델의 잎(leaf)에서 루트로 진행할 때 성립합니다. 다시 말해, 변수를 잎에서부터 루트 방향으로 제거하면 연산의 복잡도가 네트워크의 크기에 선형적으로 비례한다는 것을 의미합니다.
이것은 다형트리가 특정 유형의 확률적 그래피컬 모델에서 효율적인 계산을 가능하게 하는 중요한 특성 중 하나입니다. 다형트리는 연구 및 응용 분야에서 확률적 모델링 및 추론에 유용하게 사용됩니다.
Approximate Inference
근사 추론(Approximate Inference)은 확률적 그래피컬 모델에서 정확한 확률 분포를 계산하는 것이 어려운 경우, 더 효율적인 방법으로 확률 분포를 근사하는 기술을 나타냅니다. 확률적 그래피컬 모델은 변수 간의 상호작용을 표현하는데 사용되며, 베이지안 네트워크나 마르코프 랜덤 필드와 같은 모델을 포함합니다.
근사 추론은 다음과 같은 상황에서 유용합니다:
- 복잡한 모델: 모델이 매우 복잡하고 변수가 많은 경우, 정확한 추론이 계산상 현실적으로 불가능할 수 있습니다. 근사 추론은 계산 비용을 줄이면서 결과를 얻을 수 있도록 도와줍니다.
- 대규모 데이터: 대규모 데이터셋에서 추론을 수행하는 경우, 정확한 추론은 많은 계산 리소스를 필요로 할 수 있습니다. 근사 추론은 데이터를 기반으로 빠르게 추론을 수행할 수 있습니다.
- 추론의 빈도: 실시간으로 추론을 수행해야 하는 경우 정확한 추론은 시간 제약을 갖게 됩니다. 근사 추론은 빠른 응답을 제공할 수 있습니다.
근사 추론에는 여러 기술이 포함될 수 있으며, 일반적인 방법으로는 다음과 같은 것들이 있습니다:
- 몬테 카를로 샘플링(Monte Carlo Sampling): 확률적 샘플링을 사용하여 확률 분포를 근사합니다. Markov Chain Monte Carlo (MCMC) 및 중요한 샘플링 등이 여기에 속합니다.
- 변분 추론(Variational Inference): 본질적으로 근사 확률 분포를 사용하여 원래 분포와의 차이를 최소화합니다.
- 근사 베이지안 네트워크(Approximate Bayesian Networks): 정확한 베이지안 네트워크 대신 더 간단한 네트워크를 사용하여 추론을 수행합니다.
- 베이지안 근사(Bayesian Approximation): 추론 대신 베이지안 근사를 사용하여 분포를 추정합니다.
근사 추론은 정확성을 희생하면서 계산 비용을 줄이는 방법으로, 많은 실제 응용 분야에서 유용하게 사용됩니다. 그러나 주의해야 할 점은 추론 결과가 근사치임을 인식하고 해당 결과를 신뢰할 수 있는지 검증해야 한다는 것입니다.
Quick Warm-Up
- 우리가 알지 못하는 어떤 확률 𝑝로 앞면이 나오는 편향된 동전이 있다고 가정해봅시다. 이 동전을 사용하여 0과 1의 정확한 확률이 0.5인 무작위 비트(random bits)를 어떻게 생성할 수 있을까요?
- 답변 (von Neumann):
- 동전을 두 번 던져서, 결과가 다를 때까지 반복합니다.
- HT = 0, TH = 1이라고 정의하며, 각각의 결과가 나올 확률은 𝑝(1−𝑝)입니다.
이 빠른 복습에서 언급한 내용은 "von Neumann" 방법이라고도 알려진 확률적 비트 생성 방법에 관한 것입니다. 이 방법은 편향된 동전으로부터 정확한 확률이 0.5인 무작위 비트를 생성하는 방법입니다. 아래에서 이 방법을 설명합니다:
- 먼저, 주어진 편향된 동전을 두 번 던집니다.
- 두 번의 동전 던지기 결과가 서로 다른 경우, 즉 "HT" 또는 "TH"인 경우에만 고려합니다.
- "HT"가 나온 경우, 이를 0으로 해석하고 "TH"가 나온 경우에는 이를 1로 해석합니다.
- 각각의 경우에 대한 확률을 고려하면, "HT"가 나올 확률은 𝑝(1−𝑝)이고 "TH"가 나올 확률도 마찬가지로 𝑝(1−𝑝)입니다.
이 방법은 편향된 동전을 사용하여 정확한 확률 0.5로 0 또는 1을 생성하는 간단하면서도 효과적인 방법입니다. 두 번의 동전 던지기를 통해 결과가 서로 다른 경우만을 고려하므로, 생성된 비트는 정확한 확률 0.5로 근사됩니다.
Sampling
기본 아이디어
- 샘플링 분포 𝑆에서 𝑁개의 샘플을 추출합니다.
- 근사 사후 확률을 계산합니다.
- 이것이 실제 확률 𝑃로 수렴함을 보여줍니다.
왜 샘플링을 사용할까요?
- 종종 빠른 시간 안에 괜찮은 근사 답을 얻을 수 있습니다.
- 알고리즘은 매우 간단하고 일반적이며(고급 모델에 적용하기 쉬움), 메모리를 거의 사용하지 않습니다(𝑂(𝑛)).
- 정확한 알고리즘은 큰 모델에 적용하기 어려울 때도 샘플링은 적용 가능합니다.
샘플링은 확률적인 모델에서 확률 분포를 근사하는 방법 중 하나로, 다음과 같은 기본 아이디어에 기반합니다:
- 샘플링 분포 𝑆에서 𝑁개의 샘플을 무작위로 추출합니다.
- 이 추출한 샘플을 사용하여 원하는 확률 분포나 사후 확률 분포를 근사합니다.
- 충분한 수의 샘플을 추출하면, 이 근사치가 실제 확률 분포에 수렴함을 보일 수 있습니다.
샘플링을 사용하는 이유는 다음과 같습니다:
- 종종 빠른 시간 안에 정확한 답변을 얻을 수 있습니다. 특히 정확한 계산이 어려운 복잡한 문제에서 유용합니다.
- 샘플링 알고리즘은 매우 간단하고 일반적입니다. 다양한 모델에 적용하기 쉽습니다.
- 샘플링 알고리즘은 메모리를 매우 적게 사용합니다. 이것은 대규모 모델이나 데이터에 대한 계산에서 중요한 요소입니다.
- 정확한 알고리즘은 대형 모델에서 계산 비용이 급격하게 증가하는 경우가 많습니다. 하지만 샘플링은 큰 모델에도 적용 가능하며, 복잡도가 선형적으로 증가하므로 대용량 모델에도 효과적입니다.
따라서 샘플링은 복잡한 확률 모델에서 빠르고 효율적인 근사화를 위한 강력한 도구로 사용됩니다.
Example
- 두 개의 에이전트 프로그램 𝐴와 𝐵가 몬폴리 게임(Monopoly)을 하는 상황을 가정해보겠습니다.
- 𝐴가 이길 확률은 얼마일까요?
- 방법 1:
- 𝑠를 주사위 굴리기와 찬스 및 커뮤니티 체스트 카드 시퀀스로 정의합니다.
- 주어진 𝑠에 대해 결과 𝑉(𝑠)가 결정됩니다(이긴 경우 1, 진 경우 0).
- 𝐴가 이길 확률은 ∑2_𝑠▒〖𝑃(𝑠)𝑉(𝑠)〗입니다.
- 문제: 무한한 수의 시퀀스 𝑠가 존재합니다!
- 방법 2:
- 𝑃(𝑠)에서 𝑁개의 시퀀스를 샘플링하고, 𝑁개의 게임(예를 들어 100번)을 플레이합니다.
- 𝐴가 이길 확률은 대략 1/𝑁 ∑2_𝑖▒〖𝑉(𝑠_𝑖)〗, 즉 샘플에서 이긴 비율입니다.
- 방법 1:
이 예시에서는 몬폴리 게임(Monopoly)에서 두 개의 에이전트 프로그램인 𝐴와 𝐵 중에서 𝐴가 이길 확률을 계산하는 방법에 대해 설명하고 있습니다.
- 방법 1:
- 먼저, 가능한 주사위 굴리기와 찬스 및 커뮤니티 체스트 카드 시퀀스를 나타내는 𝑠를 정의합니다.
- 이 시퀀스가 주어진 경우, 게임의 결과인 𝑉(𝑠)가 결정됩니다. 이 때, 𝑉(𝑠)가 1인 경우는 𝐴가 이긴 경우를 나타내며, 0인 경우는 𝐴가 지는 경우를 나타냅니다.
- 그런 다음, 모든 가능한 시퀀스 𝑠에 대한 확률을 고려하여 𝐴가 이길 확률을 계산합니다. 이것은 ∑2_𝑠▒〖𝑃(𝑠)𝑉(𝑠)〗로 나타낼 수 있습니다.
- 그러나 이 방법의 문제점은 무한한 수의 가능한 시퀀스가 존재하기 때문에 계산이 어렵습니다.
- 방법 2:
- 이 방법은 확률 분포 𝑃(𝑠)에서 𝑁개의 시퀀스를 무작위로 추출합니다. 예를 들어, 100번의 게임을 플레이하기 위해 100개의 시퀀스를 추출할 수 있습니다.
- 그런 다음, 각각의 시퀀스를 사용하여 게임을 플레이하고, 𝐴가 이긴 경우를 기록합니다.
- 최종적으로, 이 방법은 추출한 시퀀스 중에서 𝐴가 이긴 비율을 계산하여 확률을 근사합니다. 즉, 1/𝑁 ∑2_𝑖▒〖𝑉(𝑠_𝑖)〗입니다.
이 두 가지 방법 중 두 번째 방법은 확률을 근사화하기 위해 샘플링을 사용하는 방법으로, 모든 가능한 시퀀스를 고려하지 않고도 확률을 계산할 수 있으므로 효율적입니다.
Sampling Basics: Discrete (Categorical) Distribution( 샘플링 기초: 이산(범주형) 분포)
- 편향된 𝑑면 주사위 𝑃(𝑥)를 시뮬레이션하기 위한 단계:
- 단계 1: [0, 1) 범위 내에서 균일 분포로부터 샘플 𝑢를 얻습니다.
- 예: 파이썬의 random() 함수를 사용
- 단계 2: 이 샘플 𝑢를 주어진 분포에 대한 결과로 변환합니다. 각 결과 𝑥_𝑖를 [0, 1) 범위의 𝑃(𝑥_𝑖) 크기의 하위 구간에 연결하여 이루어집니다.
- 단계 1: [0, 1) 범위 내에서 균일 분포로부터 샘플 𝑢를 얻습니다.

- 예시

- 만약 random() 함수가 𝑢 = 0.83을 반환한다면, 이 샘플은 C = 파랑(또는 blue)인 것입니다.
- 예를 들어, 8번 샘플링 한 후:

이 문장은 이산(범주형) 확률 분포에서 샘플링하는 기초적인 방법을 설명하고 있습니다. 이 방법을 사용하면 특정 확률 분포에 따라 무작위로 결과를 얻을 수 있습니다.
- 단계 1: [0, 1) 범위에서 균일한(uniform) 분포에서 난수(𝑢)를 생성합니다. 이는 파이썬과 같은 프로그래밍 언어에서 random() 함수를 사용하여 구현할 수 있습니다.
- 단계 2: 생성된 난수(𝑢)를 주어진 확률 분포(𝑃(𝑥))에 따른 결과로 변환합니다. 이를 위해 각각의 가능한 결과(𝑥_𝑖)를 [0, 1) 범위에서 해당 결과의 확률(𝑃(𝑥_𝑖))에 비례하는 크기의 하위 구간에 매핑합니다. 예를 들어, 만약 주사위의 결과가 {A, B, C}이고 각각의 결과에 대한 확률이 {0.2, 0.3, 0.5}라면, [0, 0.2) 구간은 A에, [0.2, 0.5) 구간은 B에, 그리고 [0.5, 1) 구간은 C에 대응됩니다.
예시:
- 만약 random() 함수가 𝑢 = 0.83을 반환한다면, 해당 샘플은 C(파랑)인 것입니다. 이것은 주어진 확률 분포에 따라 얻어진 결과 중 하나를 나타냅니다.
이 방법을 사용하면 주어진 이산 확률 분포에서 결과를 무작위로 추출할 수 있으며, 특정 결과가 발생할 확률은 해당 결과의 확률에 비례합니다.
Sampling in Bayes Nets
- 사전 샘플링 (Prior sampling)
- 거부 샘플링 (Rejection sampling)
- 우도 가중치 샘플링 (Likelihood weighting)
- 기브스 샘플링 (Gibbs sampling)
베이즈 네트워크에서 사용되는 다양한 샘플링 기술을 간단히 설명하겠습니다:
- 사전 샘플링 (Prior sampling):
- 이 방법은 베이즈 네트워크의 사전 확률 분포를 사용하여 샘플을 생성하는 방법입니다.
- 먼저 네트워크의 루트 노드부터 시작하여 순서대로 각 노드의 확률 분포를 사용하여 값을 샘플링합니다.
- 이 방법은 네트워크의 확률 분포를 따라 샘플을 생성하는데 사용됩니다.
- 거부 샘플링 (Rejection sampling):
- 거부 샘플링은 특정 조건을 만족하는 샘플을 생성하는 방법입니다.
- 주어진 증거(evidence)에 대한 조건을 만족하는 샘플만을 생성하고, 나머지는 거부합니다.
- 이 방법은 조건부 확률을 계산하거나 베이즈 네트워크의 확률 분포를 추정하는 데 사용됩니다.
- 우도 가중치 샘플링 (Likelihood weighting):
- 우도 가중치 샘플링은 거부 샘플링과 유사하지만 확률 가중치를 사용하여 샘플을 생성합니다.
- 주어진 증거에 대한 조건을 만족하는 경우에만 확률 가중치를 고려하여 값을 샘플링합니다.
- 이 방법은 베이즈 네트워크에서 조건부 확률을 추정하는 데 사용됩니다.
- 기브스 샘플링 (Gibbs sampling):
- 기브스 샘플링은 마르코프 연쇄 몬테 카를로(Markov Chain Monte Carlo, MCMC) 방법 중 하나로, 베이즈 네트워크의 조건부 확률 분포를 추정하는 데 사용됩니다.
- 기브스 샘플링은 한 번에 한 변수씩 값을 샘플링하고, 다른 변수들은 고정된 값을 가정하며 업데이트합니다.
- 이러한 반복적인 과정을 통해 조건부 확률 분포의 샘플을 생성하고, 이를 통해 확률 분포를 근사화할 수 있습니다.
이러한 샘플링 기술은 베이즈 네트워크에서 확률 분포의 근사치를 계산하거나 조건부 확률을 추정하는 데 사용됩니다. 각각의 방법은 다른 목적과 상황에 따라 선택됩니다.
Prior Sampling

설명 나중에 추가

설명 나중에 추가
For 𝑖=1, 2, …, 𝑛 (in topological order 위상 순서로 )
Sample 𝑋_𝑖 from 𝑃(𝑋_𝑖 |parents(𝑋_𝑖))
Return (𝑥_1, 𝑥_2, …, 𝑥_𝑛)
사전 샘플링(Prior Sampling)은 베이즈 네트워크에서 확률 분포를 기반으로 샘플을 생성하는 방법입니다. 이 방법은 네트워크의 노드를 위상 순서로 방문하며 각 노드에서 해당 노드의 조건부 확률 분포를 사용하여 값을 샘플링합니다.
단계:
- 네트워크의 노드를 위상 순서로 정렬합니다. 이렇게 하면 부모 노드가 항상 자식 노드보다 먼저 방문됩니다.
- 각 노드에 대해 다음을 수행합니다:
- 해당 노드의 조건부 확률 분포인 𝑃(𝑋_𝑖 |parents(𝑋_𝑖))에서 값을 샘플링합니다. 이때, 부모 노드들의 값이 필요합니다.
- 모든 노드를 방문하고 값을 샘플링한 후, 결과적으로 (𝑥_1, 𝑥_2, …, 𝑥_𝑛) 형태로 샘플된 베이즈 네트워크의 상태를 반환합니다.
이렇게 하면 네트워크의 확률 분포를 따르는 무작위 샘플을 생성할 수 있으며, 이를 통해 네트워크의 다양한 상태를 시뮬레이션할 수 있습니다. 사전 샘플링은 베이즈 네트워크에서 확률적 추론 및 확률 분포 모델링에 널리 사용되는 방법 중 하나입니다.
- 이 과정은 다음과 같은 확률로 샘플을 생성합니다: 𝑆_PS (𝑥_1,…,𝑥_𝑛)=∏2_𝑖▒〖𝑃(𝑥_𝑖 |parents(𝑋_𝑖))=𝑃(𝑥_1,…,𝑥_𝑛)〗 즉, 베이즈 네트워크의 결합 확률입니다.
- 어떤 이벤트의 샘플 수를 𝑁_PS (𝑥_1,…,𝑥_𝑛)이라고 합시다.
- 𝑁 개의 샘플로부터의 추정값은 𝑄_𝑁 (𝑥_1,…,𝑥_𝑛)=𝑁_PS (𝑥_1,…,𝑥_𝑛)/𝑁입니다.
- 그런 다음, lim┬(𝑁→∞)〖𝑄_𝑁 (𝑥_1,…,𝑥_𝑛)〗=lim┬(𝑁→∞)〖𝑁_PS (𝑥_1,…,𝑥_𝑛)/𝑁〗 =𝑆_PS (𝑥_1,…,𝑥_𝑛) =𝑃(𝑥_1,…,𝑥_𝑛) 즉, 샘플링 절차는 일관성을 가집니다.
이렇게 하면 베이즈 네트워크의 결합 확률을 효과적으로 추정할 수 있으며, 샘플 수가 무한히 많아질 때 실제 결합 확률과 수렴함을 보입니다. 이것은 샘플링 절차가 신뢰성을 가지고 있다는 것을 의미합니다.
사전 샘플링 (Prior Sampling)은 베이즈 네트워크에서 확률 분포를 사용하여 샘플을 생성하는 과정입니다. 이 과정을 통해 생성된 샘플은 베이즈 네트워크의 결합 확률 분포를 따릅니다.
이때, 𝑆_PS (𝑥_1,…,𝑥_𝑛)는 생성된 샘플의 확률 분포를 나타내며, 이것은 베이즈 네트워크의 결합 확률과 동일합니다.
또한, 𝑁_PS (𝑥_1,…,𝑥_𝑛)은 특정 이벤트(조건)의 샘플 수를 나타냅니다. 𝑄_𝑁 (𝑥_1,…,𝑥_𝑛)은 𝑁 개의 샘플로부터의 확률 분포 추정값이며, 이는 𝑁_PS (𝑥_1,…,𝑥_𝑛)를 𝑁으로 나눈 것입니다.
이러한 샘플링 과정을 통해 생성된 샘플 수가 무한히 많아질 때, 샘플링 절차가 실제 결합 확률 분포 𝑃(𝑥_1,…,𝑥_𝑛)에 수렴함을 보이며, 이것은 샘플링 절차의 일관성을 의미합니다. 즉, 사전 샘플링은 베이즈 네트워크의 결합 확률을 효과적으로 추정하기 위한 안정적인 방법 중 하나입니다.
Example

- 베이즈 네트워크에서 여러 개의 샘플을 얻습니다:
| c | ¬s | r | w |
| c | s | r | w |
| ¬c | s | r | ¬w |
| c | ¬s | r | w |
| ¬c | ¬s | ¬r | w |
- 만약 𝑃(𝑊)를 알고 싶다면,
- 우리는 <𝑤:4, ¬𝑤:1>과 같은 카운트를 가지고 있습니다.
- 정규화(normalize)를 통해 𝑃(𝑊)= <𝑤:0.8, ¬𝑤:0.2>를 얻을 수 있습니다.
- 더 많은 샘플을 사용하면 실제 분포에 더 가까운 결과를 얻을 수 있습니다.
- 𝑃(𝐶|𝑤), 𝑃(𝐶|𝑟,𝑤), 𝑃(𝐶|¬𝑟, ¬𝑤)에 대해서는 어떨까요?
이 예시에서는 베이즈 네트워크에서 얻은 샘플을 사용하여 다양한 조건부 확률을 추정하는 방법을 설명합니다.
- 𝑃(𝑊):
- 𝑊의 확률을 추정하기 위해 <𝑤:4, ¬𝑤:1>과 같은 카운트를 사용합니다.
- 이 카운트를 정규화(normalize)하여 확률 분포를 얻습니다.
- 예를 들어, 정규화를 통해 𝑃(𝑊)= <𝑤:0.8, ¬𝑤:0.2>와 같은 결과를 얻을 수 있습니다.
- 𝑃(𝐶|𝑤):
- 𝐶가 주어졌을 때 𝑊의 조건부 확률을 추정합니다.
- 이를 위해 샘플에서 𝑊가 𝑤인 경우와 아닌 경우를 분리하여 각각의 조건부 확률을 추정할 수 있습니다.
- 𝑃(𝐶|𝑟,𝑤):
- 𝑅(루트)와 𝑊가 주어졌을 때 𝐶의 조건부 확률을 추정합니다.
- 마찬가지로 샘플에서 𝑅과 𝑊의 값이 주어진 경우를 분리하여 조건부 확률을 추정합니다.
- 𝑃(𝐶|¬𝑟, ¬𝑤):
- 루트(𝑅)와 𝑊가 아닌 경우, 즉 루트와 𝑊가 모두 발생하지 않는 경우에 𝐶의 조건부 확률을 추정합니다.
- 이 역시 샘플에서 해당 조건을 충족하는 경우를 분리하여 조건부 확률을 추정합니다.
이렇게 다양한 조건에서의 확률을 추정하려면 충분한 수의 샘플을 사용하여 확률 분포를 효과적으로 추정해야 합니다. 더 많은 샘플을 사용하면 추정 결과가 더 정확해집니다.