Outline
Uncertain outcomes ( 불확실한 결과)
Expectimax search( Expectimax 탐색 )
Other game types ( 다른 게임 유형 )
Monte Carlo tree search ( Monte Carlo 트리 탐색)
Uncertain outcomes ( 불확실한 결과)
Worst-Case vs. Average Case
아이디어: 적대적인(adversary) 상황이 아닌 우연에 의해(by chance) 결정되는 불확실한 결과(uncertain outcome)!
Expectimax Search ( 기대값 최대화 검색 )

행동의 결과를 왜 알 수 없을까요?
- 명시적(explicit) 무작위성: 주사위를 굴리기
- 예측할 수 없는 상대: 유령들이 무작위로 반응
- 행동이 실패할 수 있음: 로봇을 움직일 때, 바퀴가 미끄러질 수 있음
값들은 이제 worst-case (minimax) 결과가 아닌 average-case (expectimax) 결과를 반영해야 합니다.
기대값 최대화 검색(Expectimax Search): 최적(optimal)의 플레이에서의 평균 점수 계산
- minimax 검색처럼 최대 노드
- 기회(chance) 노드는 최소(min) 노드와 비슷하지만 결과는 확실하지 않음
- 그들의 기대 효용(expected utilities)을 계산
- 즉, 자식들의 가중평균 (기대값)을 취하십시오
나중에, 우리는 기본적인 불확실한 결과 문제를 마르코프 결정 과정(Markov Decision Processes)으로 어떻게 공식화하는지 배울 것입니다.
Expectimax Pseudocode

- value(state): 주어진 상태의 최적의 값을 반환합니다. 이 값은 상태가 터미널 상태인지, 최대화 노드인지, 아니면 기대값 노드인지에 따라 다릅니다.
- exp-value(state): 기대값 노드의 값을 계산합니다. 기대값은 상태의 모든 후속 상태에 대한 확률적 평균입니다. 여기서 각 후속 상태에 대한 확률을 곱한 후 모든 후속 상태의 값을 합산합니다.
- max-value(state): 최대화 노드의 값을 계산합니다. 이는 상태의 모든 후속 상태 중 최대값을 선택합니다.

Expectimax Example

Expectimax Pruning?

"Expectimax Pruning"은 일반적인 Expectimax 알고리즘에 있어서 표준적인 용어나 접근 방법이 아닙니다. 기본 Expectimax 알고리즘은 결정적이지 않은 환경에서 최적의 결정을 찾기 위한 것입니다. 그것은 최대화 노드 (Max nodes)와 기대값 노드 (Expectation nodes 또는 Chance nodes)를 모두 고려합니다.
Minimax 알고리즘에 대해서는 "Alpha-Beta Pruning"이라는 최적화 기법이 잘 알려져 있습니다. 이 기법은 불필요한 탐색을 제거하여 알고리즘의 효율성을 향상시킵니다. 그러나 Expectimax에 직접적으로 적용되는 Alpha-Beta Pruning 같은 기법은 존재하지 않습니다.
※ 모든 utility가 expected utility에 영향을 미치기 때문에 pruning을 할 수는 없다.
Depth-Limited Expectimax ( 깊이 제한 Expectimax)
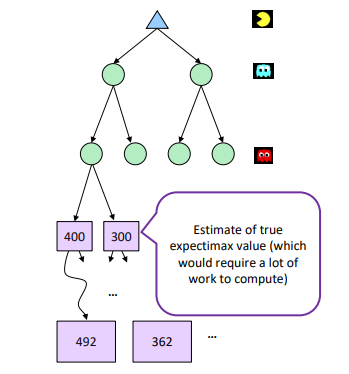
통상 게임은 위 예제처럼 1~2턴만에 끝나지 않는다. 하지만 Terminal state까지 예측을 하기에는 computing resource에 제한이 있기 때문에 통상 Tree Depth에 제한을 두는데 이 방법을 Depth-Limit Search라 한다. 말 그대로 Tree의 최대 깊이를 미리 정하고 Terminal state가 아닌 곳에서 멈추게 하는 것이다. 여기서 Depth의 의미는 앞을 내다 보는 수이다. MAX, MIN 이 1번씩 나오는 것을 1 depth라 했을 때 depth를 3으로 제한하면 앞의 3수까지 내다보고 게임 하는 것을 의미한다.
어찌됐든 결국 Terminal state가 아닌 곳에서 멈추기 때문에 non-terminal state가 terminal state와 얼마나 가까운지를 approximately 하게 알 수 있는 지표가 필요하다. 이 역할을 하는 것이 Evaluation function 이다.
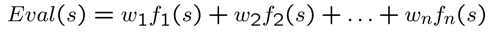
Evaluation function은 feature들의 weighted sum으로 나타내는데, 이때 feature는 경험을 토대로 (Domain 지식을 토대로) State로 부터 대략적인 점수를 부여할 수 있어야 한다. 예를 들어 Chess 게임의 경우 play의 남은 룩의 수, 퀸의 위치 등 게임에 승패를 나타내는 지표가 될 수 있다. (일종의 Heuristics function이며 A* 의 Heuristics와 유사하다.)
Probabilities(확률)
Reminder: Probabilities
랜덤 변수( random variable )는 결과가 알려지지 않은 사건을 나타냅니다.
확률 분포( probability distribution )는 결과에 가중치를 할당하는 것입니다.
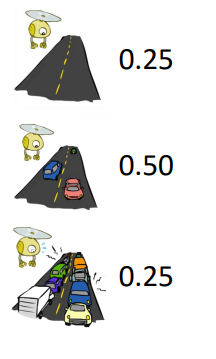
예시: 고속도로의 교통
- 랜덤 변수: T = 교통이 있는지 없는지
- 결과: T는 {없음, 가볍게, 심하게} 중 하나
- 분포: P(T=없음) = 0.25, P(T=가볍게) = 0.50, P(T=심하게) = 0.25
확률의 몇 가지 법칙 (나중에 더):
- 확률은 항상 0 이상입니다.
- 모든 가능한 결과에 대한 확률 합은 1이다.
더 많은 증거를 얻으면 확률은 변경될 수 있습니다:
- P(T=심하게) = 0.25, P(T=심하게 | 시간=오전 8시) = 0.60
- 나중에 확률을 추론하고 업데이트하는 방법에 대해 이야기하겠습니다.
Reminder: Expectations
랜덤 변수의 함수의 기대값은 결과에 대한 확률 분포에 의해 가중된 평균입니다.
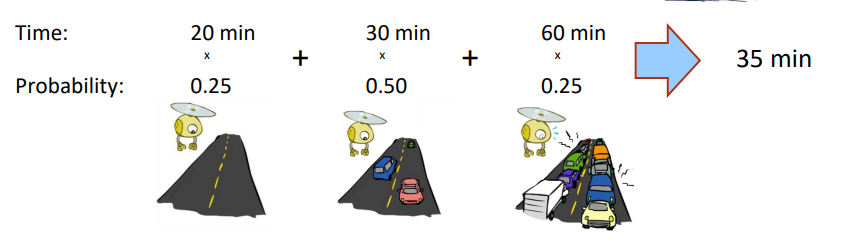
예시: 공항에 가기까지 얼마나 걸릴까요?
What Probabilities to Use?( 어떤 확률을 사용해야 할까?)
- Expectimax 검색에서는 상대방 (또는 환경)이 어떠한 상태에서 어떻게 행동할지에 대한 확률적 모델을 가지고 있습니다.
- 모델은 단순한 균일 분포일 수 있습니다 (주사위 굴리기).
- 모델은 복잡하고 많은 계산을 필요로 할 수 있습니다.
- 우리의 제어 범위 밖의 결과에 대한 확률 노드를 가지고 있습니다: 상대방 또는 환경.
- 모델은 적대적인 행동이 가능성이 높다고 말할 수 있습니다!
- 지금은 각 확률 노드가 그 결과에 대한 분포를 지정하는 확률로 마법처럼 동반된다고 가정합니다.
다른 에이전트의 행동에 대한 확률론적 믿음을 가지고 있다는 것은 그 에이전트가 동전을 던지고 있다는 것을 의미하지 않습니다!
Quiz: Informed Probabilities ( 정보를 바탕으로 한 확률)
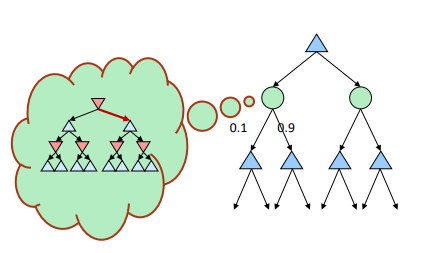
- 상대방이 실제로 2단계 깊이의 minimax를 실행하고 있으며, minimax의 결과를 80%의 확률로 사용하고 나머지 시간에는 무작위로 움직인다고 가정해봅시다.
질문: 어떤 트리 검색을 사용해야 합니까?
답변: 기대값 최대화 (Expectimax)!
- 각 기회 노드의 확률을 파악하기 위해서는 상대방의 시뮬레이션을 실행해야 합니다.
- 이런 종류의 작업은 매우 빠르게 속도가 느려집니다.
- 상대방이 당신을 시뮬레이션하는 것을 시뮬레이션해야 한다면 더욱 나빠집니다...
- ...단, minimax는 하나의 게임 트리로 모두 축소되는 좋은 특성이 있습니다.
예를 들어 상대가 80%는 depth 2 minimax를 돌려서 선택하고, 20%는 랜덤으로 선택한다고 하자.
그럼 MAX는 상대방의 행동을 결정하기 위해 depth 2 minimax를 돌려야 한다.
이를 통해 구한 방향에 0.8을 주고, 20%는 랜덤으로 선택한다고 했으므로 공평하게 나눠서 각 방향에 0.1씩 주면 될 것이다.
이런 식의 탐색 안의 탐색은 optimal하긴 하나, 정말 느리다.
Depth 2라서 다행이지, 깊이 제한 없이 탐색한다고 가정하면 그냥 탐색이 끝나지 않을 수도 있다.
'전공 공부 > 인공지능(Artificial Intelligence)' 카테고리의 다른 글
| [인공지능] Reinforcement Learning II - 1 (0) | 2023.11.06 |
|---|---|
| [인공지능] Markov Decision Processes I - 1 (0) | 2023.10.25 |
| [인공지능] Adversarial Search 1 - 4 (0) | 2023.10.16 |
| [인공지능] Adversarial Search 1 - 3 (0) | 2023.10.16 |
| [인공지능] Adversarial Search 1 - 2 (0) | 2023.10.16 |



